knigechka: СИНТЕЗ КОМБИНАЦИОННЫХ И НАКАПЛИВАЮЩИХ СЧЕТЧИКОВ

Различают комбинационные и накапливающие счетчики. Комбинационный счетчик – это комбинационная схема, формирующая на своих выходах код (целое двоичное число), который больше (меньше) входного кода на целое число . Как правило, , где Накапливающий счетчик – это последовательностная схема (схема с памятью), которая в каждом такте счета увеличивает (уменьшает) код своего состояния на целое число, не обязательно являющееся степенью двойки. Схемы счетчиков, изменяющих свое состояние на целое число, не являющееся степенью двойки, будут рассмотрены на практическом занятии, посвященном двоичным сумматорам.

Пример 2. Спроектировать четырехразрядный комбинационный инкрементирующий (суммирующий) двоичный счетчик, т.е. комбинационную схему, выполняющую микрооперацию В(1:4):= A(1:4)+1, где A(1:4) – входы схемы, B(1:4) – выходы схемы. Старшим считается первый разряд счетчика.

Синтезируем схему типового i-го разряда счетчика (рисунок 9,а) и наберем из этих схем требуемую разрядность счетчика, как это показано на рисунке 9,б Подобный подход - один из основных подходов при синтезе операционных элементов.

На входы i-го разряда счетчика (рисунок 9,а) поступают сигналы a_i –

i-ый разряд входного кода А и p_i– перенос (в вычитающем счетчике – заем) в этот разряд из предыдущего младшего разряда счетчика. Счетчик суммирует два указанных сигнала и выдает на выход два сигнала – b_i(i-ый разряд выходного кода В) - сумма входных сигналов, p_i_-1 – перенос (заем) в следующий старший разряд. Перенос в самый младший разряд n-разрядного счетчика (рисунок 9,б) p_nравен 1, т.к. счетчик выполняет функцию прибавления (декрементирующий счетчик – вычитания) единицы из младшего разряда. Перенос (заем) из старшего разряда p₀может быть использован для наращивания разрядности счетчика.

Зависимость выходов одноразрядного суммирующего счетчика от входов приведена в таблице 5. Подобная информация для вычитающего счетчика приведена в таблице 6.

Таблица 5 Таблица 6

a_i	p_i	b_i	p_i-1	a_i	p_i	b_i	p_i_-1
0	0	0	0	0	0	0	0
0	1	1	0	0	1	1	1
1	0	1	0	1	0	1	0
1	1	0	1	1	1	0	0

Выходные сигналы для одноразрядного суммирующего счетчика вычисляются по формулам:

;

Аналогичные формулы для вычитающего счетчика:

;

Анализ приведенных формул позволяет сделать заключение о том, что сигнал b_iвычисляется одинаково как в суммирующем, так и в вычитающем счетчике (сложение по модулю два сигналов a_iи p_i).

Суммирующий счетчик отличается от вычитающего только тем, что в нем значение выходного сигнала p_i_-1 зависит от прямого значения входного сигнала a_i, а в вычитающем – от инверсного.

Перенос в самый младший разряд как вычитающего, так и суммирующего счетчикадолжен бытьтождественно равен 1 (p_n =1), чтобы выполнялась микрооперация счета.

С учетом этого

для суммирующего счетчика и

для вычитающего счетчика.

Следовательно, самый младший разряд комбинационного счетчика может быть реализован с помощью инвертора.

Важно понимать, что в суммирующем счетчике перенос в следующий старший разряд определяется прямыми значениями a_iвсех предыдущих младших разрядов, а в вычитающем - инверсными. В следующих примерах как при сложении так и при вычитании переносы во все разряды счетчика равны 1.

Перенос в вычитающем счетчике называют заемом, что не принципиально при построении электрической схемы.

Различают комбинационные счетчики с последовательным (сквозным) и параллельным переносом. В счетчиках с последовательным переносом для вычисления сигнала используется формула для суммирующего счетчика, для вычитающего счетчика.

В счетчиках с параллельным переносом для вычисления сигнала p_i_-1 используется формула для суммирующего счетчика, для вычитающего счетчика (эти две формулы логически эквивалентны двум предыдущим формулам соответственно). Схема с последовательным переносом имеет меньшую сложность (2 входа элемента «И» для реализации переноса в каждый разряд, начиная с (n-2)-го). Недостаток схемы – сравнительно невысокое быстродействие (значение выходного кода станет действительным только после того как входной сигнал пройдет через все логические элементы, формирующие переносы). Платой за высокое быстродействие схемы с параллельным переносом (задержка формирования переноса в любой разряд, начиная с (n-2)-го, равна задержке одного элемента, формирующего перенос) является увеличение сложности (число входов элемента «И», формирующего перенос возрастает с увеличением номера разряда счетчика).

Схема четырехразрядного комбинационного инкрементирующего (суммирующего) двоичного счетчика с последовательным переносом приведена на рисунке 10.

Компромиссное решение между количеством используемого оборудования и быстродействием счетчика может быть получено при использовании принципа групповой организации переноса между разрядами счетчика. В этом случае n-разрядный счетчик разбивается на последовательность групп, по m соседних разрядов в каждой группе. В пределах разрядов одной группы переносы вырабатываются параллельно для всех разрядов групп, а между группами переносы распространяются последовательно [1].

В ОА для решения ряда задач могут использоваться реверсивные комбинационные счетчики. Такой счетчик выполняет две микрооперации:

y1: B(1:n) := A(1:n) +1, y2: B(1:n) := A(1:n) – 1 .

Значения выходных сигналов такого счетчика могут вычисляться, например, по следующим функциям:

, ,

где – перенос в i-ый разряд счетчика при сложении,

– перенос в i-ый разряд счетчика при вычитании (так называемый заем),

– сигнал, суммирующий перенос и заем в соответствующих разрядах счетчика с учетом поданного в схему управляющего сигнала.

Теперь рассмотрим накапливающие счетчики, выполняющие микрооперацию (инкрементирующий), микрооперацию (декрементирующий), обе микрооперации (реверсивный). Анализ реализуемых функций позволяет сделать вывод о том, что накапливающий счетчик – это схема, содержащая элементы памяти.

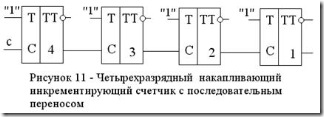
В качестве примера на рисунке 11 приведена функциональная схема четырехразрядного суммирующего счетчика с последовательным переносом. В накапливающих счетчиках последовательный перенос отличается от сквозного.

Типовым разрядом комбинационного счетчика является Т-триггер в счетном режиме. Таблица истинности T- триггера – таблица 7. Для обеспечения счетного режима работы триггеров (т.е. режима переключения в противоположное состояние по каждому импульсу, поступающему на синхровход) в соответствии с таблицей 7 на входы T всех триггеров подана логическая 1. Сигналы межразрядных переносов поданы на С-входы соответствующих триггеров.

Таблица 7

T(t)	C(t)
0	c
1	c

Вычитающий счетчик будет отличаться от суммирующего только тем, что перенос в следующий старший разряд будет определяться инверсным значением предыдущих разрядов (то есть в данном случае сигнал переноса будет сниматься не с прямого, а с инверсного выхода соответствующего триггера).

Результат микрооперации счета является действительным через промежуток времени t_счета = 4t_трс момента подачи в схему синхроимпульса , где t_тр – время переключения триггера. Это объясняется тем, что триггеры срабатывают последовательно.

Для увеличения быстродействия счетчика применяются схемы со сквозным и параллельным переносом. В этих схемах синхросигнал подается параллельно на С-входы всех триггеров, т.е. все триггеры переключаются одновременно. К моменту переключения триггеров на логических элементах формируются межразрядные переносы по формуле:

, i = n, n-1, n-2,…1 (для n- разрядного счетчика со сквозным переносом),

(для n- разрядного счетчика с параллельным переносом), где T_i – вход i-го триггера, Q_i – выход i-го триггера.

Приведенные выше формулы справедливы для суммирующих счетчиков. В соответствующие формулы для вычитающих счетчиков сигналы войдут с инверсией. Функциональная схема четырехразрядного вычитающего счетчика со сквозным переносом приведена на рисунке 12. В этой схеме

t_счета = t_тр+2t_кс, где t_кс- время задержки комбинационной схемы, формирующей сигнал переноса. Для счетчика с параллельным переносом t_счета = t_тр+ t_кс.

В схеме на рисунке 12 межразрядные переносы подаются на Т-входы триггеров. Предложите другие варианты построения подобных схем.

Достоинства и недостатки схем со сквозным, параллельным и групповым переносом обсуждались выше при рассмотрении комбинационных счетчиков.

Пример 3. Синтезировать четырехразрядный инкрементирующий накапливающий двоичный счетчик по модулю десять. Тип переноса – параллельный. Элементная база - триггеры К155ТВ1.

Кроме микрооперации счета операционный элемент должен выполнять микрооперацию сброса у0: С(1:4):=0000 и установки у1: С(1:4):=0101 и выдавать осведомительный сигнал x=(С(1:4):=0000).

Условно-графическое обозначение (УГО) микросхемы К155ТВ1 приведено на рисунке 13.

Состояния триггера К155ТВ1 приведены в таблице 8. J-K-триггер является синхронным двухступенчатым. Первая ступень синхронизируется прямым значением синхросигнала и, следовательно, срабатывает по нарастающему фронту синхроимпульса (будем называть его просто фронтом), вторая ступень синхронизируется инверсным значением синхросигнала и соответственно срабатывает по ниспадающему фронту синхроимпульса (будем называть его срезом). Следовательно, переключение J-K- триггера осуществляется по ниспадающему фронту (срезу) синхроимпульса (это необходимо учитывать при построении временных диаграмм счета).

Преимущество двухступенчатых элементов памяти состоит в том, что момент приема информации со входов на триггер (срабатывание первой ступени) и момент выдачи информации на выходы триггера (срабатывание второй ступени) разделены во времени (на время длительности синхроимпульса минус время срабатывания первой ступени триггера). Это позволяет схемам, в которых используется двухступенчатая память, работать устойчиво, когда один и тот же запоминающий элемент (триггер) в одном и том же такте является и источником и приемником информации. Примером может служить рассматриваемая схема счетчика. По фронту синхроимпульса в схеме счетчика переключатся первые ступени всех триггеров в соответствии со сформированными на логических элементах (вентилях) сигналами межразрядных переносов (длительность синхроимпульса должна быть больше, чем время переключения первой ступени триггеров). Переключение осуществится корректно, т. к. во время длительности синхроимпульса информация на выходах триггеров (выходах второй ступени), используемых для вычисления сигналов переноса, не изменяется. По срезу синхроимпульса информация с первой ступени триггеров перепишется на вторую ступень. Следующее срабатывание схемы произойдет по следующему синхроимпульсу.

Логика работы асинхронного RS-триггера микросхемы К155ТВ1 совпадает с описанной выше для микросхемы К155ТМ2.

Таблица 8


X	X	X	0	0	Не определено
X	X	X	0	1	0
X	X	X	1	0	1
0	X	X	1	1
1	0	0	1	1
1	0	1	1	1	0
1	1	0	1	1	1
1	1	1	1	1

На основе анализа таблиц 7 и 8 можно обосновать организацию T-входа триггера путем объединения J и K входов. При таком объединении на J и K вход триггера будет поступать один и тот же сигнал. Если этот сигнал равен нулю, триггер хранит свое состояние, в противном случае триггер переключается в противоположное состояние согласно таблице 8. Пусть микрооперация счета инициируется управляющим сигналом y2. Тогда для организации параллельного переноса на С-входы всех триггеров необходимо подать сигнал , а T-входы использовать для подачи межразрядного переноса.

Обычный суммирующий четырехразрядный двоичный счетчик автоматически устанавливает комбинацию 0000 после комбинации 1111 (15 в двоичной системе). Это счетчик по модулю 16.

Суммирующий двоичный счетчик по модулю 10 (основание системы счисления) должен считать от 0000 до 1001 (9 в двоичной системе счисления), а затем сбрасываться в 0000. Сброс счетчика можно осуществлять по установочным RS входам при помощи сигнала x_mod= (C(1:4)=1010). При этом комбинация 1010 будет появляться на выходах регистра кратковременно (t_тр+ t_кс) , что не повлияет на логику работы схемы, хотя может сказаться на надежности. Другими словами, при переходе счетчика из состояния 1001 в состояние 0000 через состояние 1010, присутствующее на выходах счетчика в течение времени выработки осведомительного сигнала и времени переключения триггеров, на выходе Q3 возникает кратковременный остроконечный импульс, вызывающий переходный процесс .

Построим таблицу зависимости функций возбуждения RS входов от управляющих сигналов и сигнала x_mod (таблица 9).

Таблица 9

y	R1	S1	R2	S2	R3	S3	R4	S4
у0	1		1		1		1
у1	1			1	1			1
x_m_od	1		1		1		1

На основе данной таблицы строятся функции возбуждения входов, как это было показано в примере 1. Осведомительный сигнал x=(С(1:4):=0000) может быть сформирован в соответствии с функцией

Схема счетчика приведена на рисунке 14. Для удобства на УГО микросхем К155ТВ1 изображено только по одному J и К входу. Остальные входы соответствующих конъюнкций (&J и &K) не влияют на работу схемы (в ТТЛ-логике на неподключенных входах уровень логической единицы). Объясните, почему на входы JK четвертого триггера не подается никаких сигналов. Постройте временные диаграммы работы счетчика, особое внимание уделите моменту переключения в из состояния 1001 в состояние 0000 через состояние 1010 (кратковременно присутствующее на выходах счетчика).

Примечание 1 - В реальных устройствах для обеспечения помехоустойчивости не используемые входы микросхем подключаются через сопротивление 1 КОм к источнику питания +5В (не более 20 входов на один резистор).

Примечание 2 - Вычитающий счетчик по модулю 10 считает от 1001 до 0000, а затем устанавливается в 1001. Установку счетчика в состояние 1001 можно осуществлять по установочным RS входам при помощи сигнала

x_mod= (C(1:4)=1111). Недостаток организации счета по модулю при помощи RS входов рассмотрен выше.

Если для реализации счетчика используются двухступенчатые триггеры, как в рассмотренном примере, то для реализации модуля счета можно использовать синхронные (J-K) входы триггеров. Этот подход лишен недостатка, присутствующего при управлении по асинхронным установочным (R-S) входам. Управление модулем счета в суммирующем счетчике осуществляется максимально возможной цифрой (а не модулем счета), а в вычитающем счетчике – минимально возможной цифрой (т.е. нулем).

Схема суммирующего счетчика по модулю 10 с управлением по J-K входам приведена на рисунке 15.

Обычный четырехразрядный счетчик (по модулю 16) из состояния 1001 переходит в состояние 1010. Счетчик по модулю десять после состояния 1001 должен перейти в состояние 0000. Напомним, что в счетчике со сквозным или параллельным переносом сигнал переноса, переводящий (по очередному синхросигналу) схему в следующее состояние вычисляется на логических элементах исходя из текущего состояния счетчика. Поэтому, когда счетчик находится в состоянии 1001 (осведомительный сигнал равен 1) нужно сделать равным нулю перенос в третий разряд (т.е. домножить перенос в третий разряд на ) и сделать равным единице перенос в первый разряд (т.е. сложить перенос в первый разряд с ). Стратегия коррекции переносов для обеспечения модуля счета, равного 10 изображена на рисунке 16.

Замечание. Поскольку схема выработки переноса углубляется, время счета увеличивается. Оцените время счета для схемы, представленной на рисунке 15.

Подумайте, какие проблемы могут возникнуть, если использовать для организации счетчика одноступенчатые триггеры. Как их можно решить?

Поставленную в примере 3 задачу можно решить с использованием микросхемы К155ИЕ7 – четырехразрядного реверсивного двоичного счетчика в интегральном исполнении. Условно-графическое обозначение приведено на рисунке 17.

Состояния счетчика представлены в таблице 10.

Таблица 10

Режим	Входы	Выходы
		+1	-1	D1	D2	D3	D4	Q1	Q2	Q3	Q4
Сброс	1	X	X	a	X	X	X	X	0	0	0	0	1	a
Параллель-ная загрузка	0	0	X	a	0	0	0	0	0	0	0	0	1	a
0	0	a	X	1	1	1	1	1	1	1	1	a	1
Счет на увеличение	0	1	Г	1	X	X	X	X	Q(1:4) + 1	v	1
Счет на уменьшение	0	1	1	Г	X	X	X	X	Q(1:4) – 1	1	w

Синхросигналы, инициирующие микрооперации счета, подаются на входы "+1" (суммирующий) и "-1" ( вычитающий ). Состояние счетчика меняется по положительным перепадам этих сигналов (от низкого уровня к высокому). Если для счета используется один из этих входов, на другом входе следует зафиксировать напряжение высокого уровня.

Для построения счетчиков с числом разрядов, превышающим четыре, микросхема имеет выводы сигналов окончания счета: " " и "", которые подключаются соответственно к входам "+1" и "-1" последующего четырехразрядного счетчика. Дополнительной логики при последовательном соединении счетчиков не требуется.

Если счет достиг максимума (состояние 1111), с приходом следующего тактового перепада от высокого уровня к низкому на вход "+1" на выходе "" появится низкое напряжение. После возврата напряжения на тактовом входе "+1" к высокому уровню напряжение на выходе "" останется низким еще на время, соответствующее двойной задержке переключения логического элемента ТТЛ. Аналогично на выходе "" появляется напряжение низкого уровня, если на вход "-1" пришел счетный перепад низкого уровня.

Другими словами, сигнал v становится равным 0, когда после комбинации 1111 счетчик устанавливается в 0000 при счете на увеличение. Сигнал w становится равным 0, когда после комбинации 0000 счетчик устанавливается в 1111 при счете на уменьшение.

Таким образом, импульсные перепады от выходов "" и "" служат как тактовые для последующих входов "+1" и "-1" при конструировании счетчиков более высокого порядка. Такие многокаскадные соединения счетчиков не полностью синхронные, поскольку на последующую микросхему тактовый импульс передается с двойной задержкой переключения логического элемента ТТЛ.

Счет осуществляется только если на вход разрешения параллельной загрузки подано напряжение высокого уровня, а на вход сброса R - напряжение низкого уровня. Старшим считается разряд Q4.

Если на входы и R подать напряжение низкого уровня, то код, зафиксированный на параллельных входах D1-D4, загружается в счетчик и появляется на его выходах Q1-Q4 независимо от сигнала на тактовых входах "+1" и "-1".

Параллельная загрузка запрещается, если на вход сброса R подано напряжение высокого уровня. По этому сигналу на всех выходах Q1-Q4 устанавливается низкий уровень.

Операции сброса и параллельной загрузки асинхронные.

Максимальная тактовая частота для счетчика 25 МГц; время задержки распространения сигнала от входа "+1" до выхода "" 26 нс, аналогичные задержки от входа до выхода Q4 составляют 40 нс. Время действия сигнала сброса (от входа R до выходов Q) 35 нс [3].

Схема реверсивного счетчика по модулю 10, выполняющего микрооперации y0: C(1:4):=0000, y1: C(1:4):=0101,

y3: C(1:4):=C(1:4) + 1, y4: C(1:4):=C(1:4) – 1,

представлена на рисунке 18. При построении схемы использовалась таблица 11. При составлении таблицы учтено местоположение старшего разряда счетчика и установлено соответствие С(1:4) – Q(4:1).

Таблица 11

y			+1	-1	D1	D2	D3	D4
y0	1	X	X	X	X	X	X	X
y1	0	0	X	X	1	0	1	0
y2	0	1	c		X	X	X	X
y3	0	1		c	X	X	X	X
x_mod(+)	1	X	X	X	X	X	X	X
x_mod(-)	0	0	X	X	1	0	0	1

Функции возбуждения входов:

;

(для реализации выбрана эта функция, а не , так как необходимо организовать управление входом со стороны сигнала , который вырабатывается в режиме счета, а должен переключать схему в режим параллельной загрузки);