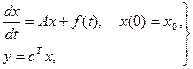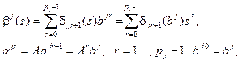Алгоритм аннулирующей редукции

Наиболее эффективным в практическом отношении методом построения минимального многочлена является метод аннулирующей редукции. Задача сводится к поиску обращающейся в ноль линейной комбинации векторов (1.40)

l, l¹=Al , l²=Al¹ , ... , l^r=Al^r- (1.40)

при минимальном их числе p+1. Указанная линейная комбинация ищется с помощью формирования векторов

l_*⁰=l, l_*¹ , l_*² , ... , l_*^r

с возрастающим числом нулевых элементов вплоть до образования нулевого вектора l_*^p, дающего соотношение (1.41)

l ^p+d₁ l ^{p -1}+d₂ l ^p-2+ ... +d_p-1 l ¹+d_p l =0 (1.41)

Алгоритму аннулирующей редукции придана удобная табличная форма.

Пусть задан вектор l и требуется построить его минимальный многочлен вида (1.42)

d(s)= s ^p+d₁ s ^p-1+d₂ s ^p-2+ ... +d_p-1 s+d_p (1.42)

Таким образом, возникает задача поиска коэффициентов линейной комбинации (1.41). Для решения этой задачи рассматривается ряд векторов l_*^r, r=0,1,2,..., l_*⁰=l, определяющихся по формуле (1.43)

l_*^r=Al_*^r-1+g_k^rl_*^k , r=1,2, (1.43)

Коэффициенты линейной комбинации (1.43) g_r^k выбираются на каждом шаге r, с учетом условия, что в каждом последующем конструируемом векторе число нулевых элементов должно возрастать.

Алгоритм начинается с первого шага r=1. Для этого в исходном векторе l выбирается элемент d, с номером m , такой что

d=l_m¹ 0 (1.44)

Составляется линейная комбинация

l_*¹=Al+g₀¹l,

коэффициент g₀¹ выбирается так, чтобы выполнялось условие

l_*¹_m=0.

Тогда он вычисляется по формуле

g₀¹=-(Al)_m / d

На втором шаге редукции при r=2 в векторе l_*¹ выбирается элемент d₁, с номером m₁¹m, такой, что

l_*¹_m1¹0

Составляется линейная комбинация

l_*²=Al_*¹+g₀²l+g₁²l_*¹ ,

коэффициенты g₀² и g₁² выбираются с учетом условий

l_*²_m= 0 , l_*²_m1= 0.

Тогда искомые коэффициенты определяются по формулам

g₀²=-(Al_*¹)_m / d

g₁²=-[(Al_*¹)_m1 +g₀² l_m1 ]/ d_1.

Выбранные элементы d и d₁ называются ведущими элементами векторов l и l_*¹ соответственно.

Далее указанная процедура продолжается индуктивно для построения векторов вида (1.43). Можно записать соотношения для полученных векторов:

1. l_*¹_m=0.

2. l_*²_m= 0 , l_*²_m1= 0.

............................................ (1.45)

r-2. l_*^r-2_m= 0 , l_*^r-2_m1= 0 , ... , l_*^r-2_{m r-3}= 0 .

r-1. l_*^r-1_m= 0 , l_*^r-1_m1= 0 , ... , l_*^r-1_{m r-3}= 0 , l_*^r-1_{m r-2}= 0 .

где m, m₁, ... , m_r-2 - номера ведущих элементов векторов l_*⁰=l, l_*¹ , l_*² , ... , l_*^r-2 соответственно.

Предположим, что на шаге r выбирается элемент d_r-1 с номером m_r-1 , причем

d_r-1= l_*^r-1_{m r-1}¹ 0

Тогда, выполняя указанную выше процедуру построения линейной комбинации и выбора коэффициентов, конструируется вектор l_*^r со всеми нулевыми компонентами.

Для удобства формирования таблицы вводятся обозначения:

f_*^r=Al_*^r-1 , r=1,2, ... (1.46)

А для векторов l_*^r будет справедливо выражение

l_*^r=f ^r+g_k^rl_*^k (1.47)

Учитывая соотношение (1.45) можно записать

l_*^r_m= f_m^r + g₀^r l_m

l_*^r_m1= f_{m 1}^r + g₀^r l_{m 1}+g₁^r l_*¹_m1

...............................................

l_*^r_mk= f_m^r_k + g₀^r l_{m k}+g₁^r l_*¹_mk+ ... +g_k^r l_*^k_mk (1.48)

...............................................

l_*^r_mr-1= f_m^r_r-1 + g₀^r l_{m r-1}+g₁^r l_*¹_mr-1+ ... +g_r-1^r l_*^r-1_mr-1

Если учесть, что на r - ом шаге редукции требуется образовать нуль-вектор, то есть выполнить условия

l_*^r_m= 0 , l_*^r_m1= 0 , ... , l_*^r_{m r-2}= 0 , l_*^r_{m r-1}= 0 , (1.49)

то из соотношения (1.48) определяются коэффициенты g_k^r :

g₀^r =-f_m^r / d

g₁^r=-(f_m1^r+g₀^r l_m1) / d₁

.........................................

g_k^r=-(f_mk^r+g₀^r l_mk+g₁^r l_*¹_mk+ ...+ g_k-1^r l_*^k-1_mk-1) / d_k (1.50)

..........................................................................

g_r-1^r=-(f_mr-1^r+g₀^r l_mr-1+g₁^r l_*¹_mr-1+ ...+ g_r-2^r l_*^r-2_mr-1) / d_r-1

Таким образом, при построении линейной комбинации векторов (1.47) с учетом выбора коэффициентов (1.50) образуется вектор l_*^r , у которого r элементов с номерами m, m₁, ... , m_r-1 равны 0. Каждый из построенных векторов l_*^r , r=1,2,... может быть представлен в виде линейной комбинации векторов l, l¹=Al , l²=Al¹ , ..., l^r=Al^r-1 вида

l_*^r =l^r+d₁l^r-1+d₂l^r-2+ ... +d_r-1l¹+d_rl (1.51)

Если при r=p вектор l_*^p равен нулю, то равенство (1.51) принимает вид (1.41). Так как это равенство по построению образуется впервые, то с учетом соотношения (1.41) формируется минимальный многочлен с коэффициентами:

d₁=d₁^p , d₂=d₂^p , ..., d_p-1= d_p-1^p, d_p=d_p^p (1.52)

Для построения таблицы вводятся обозначения:

h^r1= f ^r + g₀^r l

h^r2= h^r1+g₁^r l_*¹

..............................

h^rk= h^rk-1+g_k^r l_*^r-1 (1.53)

..............................

h^rr-1= h^rr-2+g_r-2^r l_*^r-2 , r=2,3,...

Тогда вектор l_*^r формируется по формуле

l_*^r= h^rr-1+g_r-1^r l_*^r-1 (1.54)

а соотношение (1.50) принимает вид

g₀^r =-f_m^r / l_m

g₁^r=- h^r1_m1 / l_*¹_m1

..................................

g_k^r=- h^rk_mk / l_*^k_mk (1.55)

..................................

g_r-1^r=- h^rr-1_mr-1 / l_*^r-1_mr-1 , r=2,3,...

Получая коэффициенты g_k^r из соотношений (1.53),(1.55) при k=0,1,...,r-1, можно вычислить коэффициенты линейной комбинации (1.51). Для этого подставляется выражение (1.51) в (1.40) и приравниваются коэффициенты при векторах l^r-1,l^r-2,...,l¹,l. В итоге получается соотношение

d₁^r=d₁^r-1+ g_r-1^r

d₂^r=d₂^r-2+ g_r-1^rd₁^r-1+ g_r-2^r

....................................

d_k^r=d_k^r-1+ g_r-1^rd_k-1^r-1+ g_r-2^rd_k-2^r-2+ ... +g_r-k+1^rd₁^r-k+1+ g_r-1^r (1.56)

..................................................................................

d_r-1^r=d_r-1^r-1+ g_r-1^rd_r-2^r-1+ g_r-2^rd_r-3^r-2+ ... +g₂^rd₁²+ g₁^r

d_r^r=0+ g_r-1^rd_r-1^r-1+ g_r-2^rd_r-2^r-2+ ... +g₂^rd₂²+ g₁^rd₁¹+ g₀^r

Вычислениям по соотношению ( 1.56 ) можно придать табличную форму (табл 1.1). Формируя строки, указанные в таблице, умножая их на g_k^r , при k=0,1,... указанные колонкой справа и складывая соответственно элементы этих строк по столбцам, получаются коэффициенты линейной комбинации (1.51) по найденным на предыдущих шагах.

Выполняя вычисления последовательно при r = 1, 2, ..., p в последней таблице получим коэффициенты минимального многочлена ( 1.52 ). Указанному рекурентному процессу можно придать следующую форму :

d ^r(s)= s^r + d₁^r s^r-1+ d₂^r s^r-2 + ... +d_r-1^r s + d_r^r, r = 0, 1, ..., p (1.57)

d ⁰(s)= 1

Таблица 1.1

k	sr sr-1 sr-2 sr-3 ... s2 s1 s0	gkr
0 1 2 ... r-1 r	0 0 0 0 ... 0 0 1 0 0 0 0 ... 0 1 d11 0 0 0 0 ... 1 d12 d22 ................................................................................ 0 1 d1r-1 d2r-1 ... dr-3r-1 dr-2 r-1 dr-1 r-1 1 d1r-1 d 2r-1 dr-3r-1 ... dr-2 r-1 dr-1 r-1 0	g0r g1r g2r . gr-1r 1
S	1 d1r d 2r dr-3r ... dr-2 r dr-1 r dr r

Многочлены выражения ( 1.57 ) связаны рекурентным соотношением :

d ^r(s)= sd ^r-1(s)+ g_k^rd ^k(s), r = 1, 2, ... p (1.58)

где d ⁰(s)= 1.

Учитывая, что коэффициенты g_k^r определены выше, можно записать согласно (1.58) соотношение :

d₁⁰(s)= 1

d₂¹(s)= s + g¹

d₃²(s)= s d ¹(s)+ g₁² d ¹(s)+ g₃² (1.59)

..............................................

d ^r(s)= s d ^r-1(s)+ g_r-1^r d ^r-1(s)+ g_r-2^r d ^r-2(s)+ ... + g₁^r d ¹(s)+ g ^r

..............................................

на последнем шаге вычислений определяются коэффициенты минимального многочлена d (s)= d ^p(s)

d ^p(s)= s d ^p-1(s)+ g_k^pd ^k(s) (1.60 )

Полную схему вычислений для построения минимального многочлена на основе соотношений ( 1.53, 1.54, 1.56, 1.46, 1.40 ) можно представить в табличной форме ( табл. 1.2 ), представляющей собой фрагмент алгоритма на r-ом шаге.

Таблица заполняется числами * последовательно по шагам k = 0, 1, ... r. Строки левой части таблицы заполняются значениями элементов векторов, а строки правой части - значениями коэффициентов многочленов при степенях s^k , k = 0, 1, ..., n. В последней строке таблицы получаем слева компоненты l_*^r₁ , l_*^r₂ , ..., l_*^r_n вектора l_*^r , а справа коэффициенты 1, d₁ ^r, ..., d _r^r , при указанных вверху степенях многочлена d ^r(s).

Таблица 1.2

k		1 2 3 ... n	dk	gkr	sr sr-1 ... s2 s1 s0
0 1 2 . r-1	f r g0rl h r1 g1 r l*1 hr2 g2r l*2 ... hrr-1 gr-1r l*r-1	* * * ... * * * * ... * * * * ... * * * * ... * * * * ... * * * * ... * .................. * * * ... * * * * ... *	* * * . *	* * * . *	* * * * * * ................................ * ... * * * 1 * ... * * *	g0 r d o(s) g01r d 1(s) g2 r d 2(s) ...... gr-1r d r-1(s) sd r-1(s)
r	l*r	* * * ... *			1 * ... * * *	d r(s)

По описанному в данном подразделе алгоритму аннулирующей редукции была разработана программа построения минимального многочлена вектора относительно заданной матрицы. Описание программы приводится в подразделе описания программ.

Построение изображений заданных решений линейной системы по минимальным многочленам векторов пространства состояний

1.1.1 Будем рассматривать линейную стационарную систему, заданную во временной области уравнениями состояния и выходов

(1.1)

где x(t)ÎRⁿ вектор состояния, A - n´n заданная матрица коэффициентов, f(t) ÎRⁿ – заданная вектор функция, cÎRⁿ – вектор, определяющий выбор выхода системы y(t) )ÎR¹. Традиционные подходы к построению заданного решения системы (1.1) так или иначе связаны с задачей обращения характеристической матрицы (sI – A). Например, преобразование Лапласа системы (1.1), сразу же алгебраизируя задачу, приводит в области изображений к соотношению

Формирование представления для обратной матрицы

где D(s) – характеристический многочлен, а P(s) – присоединенная (многочленная) матрица системы, представляет собою основную часть задачи. Последующее восстановление оригинала осуществляется уже сравнительно просто с помощью “техники” разложения изображения на простейшие дроби или теории вычетов ( и здесь рассматриваться не будет). Аналогичное место принадлежит задаче представления указанной обратной матрицы и в других подходах к построению заданного решения системы (1.1). Вычисление элементов этого представления выполняется либо с помощью миноров характеристической матрицы, включая характеристический определитель, либо методами типа Фаддеева – Леверрье. С повышением размерности системы сложность вычислений быстро возрастает. К тому же дело сильно осложняется при необходимости (например, в задачах анализа неасимптотической устойчивости) устранения общих нулей числителя и знаменателя представления, т.е. приведения его к виду

где P(s) - приведенная присоединенная матрица и D(s) – минимальный многочлен матрицы A взаимно просты [1]. Известно преобразование акад. А.Н. Крылова системы (1.1), которое существенно упрощает вычисление коэффициентов характеристического многочлена и алгебраическая интерпретация Ф.Р. Гантмахера этого преобразования [1] ( там же библиография по исследованию метода). В этой интерпретации характеристический многочлен в так называемом регулярном случае строится эффективным процессом исключения типа Гаусса как минимальный многочлен произвольно взятого вектора lÎRⁿ. По существу, регулярный случай определен как такой, когда минимальный многочлен выбранного вектора совпадает с характеристическим. Если это не так ( степень минимального многочлена меньше степени n характеристического, и первый является лишь делителем второго), то метод не дает полного результата, поскольку не определена в общем виде роль минимальных многочленов векторов пространства Rⁿ â конструкции заданного решения системы. В связи со сказанным описание этой роли представляется достаточно интересным и важным и является предметом нашего последующего изложения.

1.1.2 Напомним для удобства определения и отметим необходимые для дальнейшего свойства аннулирующих и минимальных многочленов [1]. Пусть рассматривается пространство состояний Rⁿ системы с базисом e¹,…, eⁿ.

Определение 1.1 Многочлен

(1.2)

называют аннулирующим многочленом матрицы A (аннулирующим многочленом пространства Rⁿ относительно матрицы A), если

(1.3)

где I – единичная матрица. Многочлен минимальной степени в множестве аннулирующих многочленов матрицы A называют минимальным многочленом матрицы A.

Замечание 1.1 Характеристический многочленматрицы A является ее аннулирующим многочленом (теорема Кели – Гамильтона).

Определение 1.2 Пусть cÎRⁿ и c^r = Ac^r-1 = A^rc, r = 1,…, p; c⁰ = c.

Условимся в обозначении

(1.4)

Многочлен (1.2) называют аннулирующим многочленом вектора c (относительно матрицы A), если d(c) = d(A)c = 0. Многочлен минимальной степени в множестве аннулирующих многочленов вектора c называют минимальными многочленами вектора c.

Определение 1.3 Пусть c^Tr = c^Tr-1A = c^TA^r, r = 1,…, p; c^T0 = c^T.

Условимся в обозначении

(1.5)

Многочлен (1.2) называют аннулирующим многочленом вектора c^T (относительно матрицы A), если d(c^T) = c^Td(A) = 0. Многочлен минимальной степени в множестве аннулирующих многочленов вектора c^T называют минимальными многочленами вектора c^T.

Замечание 1.2 Аннулирующий многочлен d(s) вектора строки c^T относительно матрицы A тождественно совпадает с таковым для вектора столбца c относительно матрицы A^T, поскольку

(1.6)

Замечание 1.3 Пусть определены минимальные многочлены d₁(s),…, d_n(s) базисных векторов e¹,…, eⁿ пространства Rⁿ соответственно. Тогда их наименьшее общее кратное (НОК) является минимальным многочленом D(s) матрицы A

(1.7)

Замечание 1.4 Пусть d(s) минимальный многочлен какого-либо вектора строки или столбца. В ряду многочленов

(1.8)

всякий многочлен является делителем предшествующего.

Замечание 1.5 Аннулирующий многочлен матрицы A является в то же время и аннулирующим многочленом вектора cÎ Rⁿ.

1.1.3 Построению модели заданного решения в области изображений предварим следующее

Утверждение 1.1 Для всякого многочлена

(1.9)

имеет место тождество

, (1.10)

где

(1.11)

Тождество (1.10) проверяется перегруппировкой слагаемых. Многочлены (1.11) будем называть сопутствующими многочленами. Запишем уравнения состояния в изображениях по Лапласу

. (1.12)

Далее с помощью этого соотношения найдем

Умножая уравнения в указанном порядке на соответственно, складывая левые и правые части и принимая во внимание Утверждение 1.1 для многочлена (1.9), получим соотношения

(1.13)

Пусть d(s) – аннулирующий многочлен вектора строки c^T , ò.å. c^Td(A) = 0. Тогда из тождества (1.13) находим явное выражение для выхода системы

(1.14)

где векторный многочлен f(s) определен выражениями

(1.15)

в соответствии с обозначениями определения 1.2.

Замечание 1.6 В частности, в соответствии с замечаниями 1.5, 1.3 в соотношении (1.14) в качестве d(s) могут быть выбраны многочлены D(s), D(s) с соответствующим определением по соотношениям (1.15) многочлена f^T(s).

Выбирая в качестве аннулирующего многочлена минимальный вектора строки c^T, получаем следующую теорему.

Теорема 1.1 Пусть d(s) минимальный многочлен вида (1.2) вектора строки c^T; d_r(s), r = 1,..., p-1 - его сопутствующие многочлены. Тогда заданное решение системы (1.1) определяет ее выход в изображениях по Лапласу в виде (1.14), (1.15), где строка многочленов f^T(s) и многочлен d(s) взаимно просты, т.е.

(1.16)

для всякого корня многочлена d(s).

Доказательство теоремы 1.1 В связи с изложенным остается доказать последнее утверждение. Оно следует из того, что

(1.17)

Действительно, нетривиальные многочлены d₁(s),…, d_p(s) при всяком s не обращаются одновременно в нуль (см. при m = p и равных нулю значениях многочленов систему (1.11) относительно коэффициентов d₀ =1, d₁,…, d_p-1 с определителем, равным 1). Поэтому линейные комбинации в левой части неравенства также не могут обратиться в нуль в силу определения минимального многочлена (равенство повлекло бы за собою следствие о возможности построения минимального многочлена степени, меньшей чем p).

1.1.4 Пусть - переходная матрица и матричная экспонента . В силу уравнений

(1.18)

для изображения имеем

(1.19)

и

(1.20)

Последнее равенство легко усмотреть в силу экспоненциального представления переходной матрицы или, например, рассматривая матрицу

,

для которой домножением слева и справа на (sI - A) сразу находим X(s) = 0 для " s ¹ l, где l - корень характеристического многочлена det(sI-A) матрицы A. Из (1.18) следует, что "j" - столбца матрицы Ф(t) будем иметь уравнение (1.1) при f(t) = 0 и x₀ = e^j = (0...1...0)^T с единичной j - той компонентой. Пусть f^Tj(s) вектор строка многочленов, определенных соотношением (1.15) при c^T = e^iT = (0...1...0)^T с единичной i - той компонентой, и пусть f_ij(s), j = 1,..., n - компоненты этого вектора строки. Полагая в (1.14) v(s) = e^j, c^T = e^iT, находим по соотношениям (1.14), (1.15) изображение i, j - го элемента переходной матрицы

, (1.21)

где d_i(s) - минимальный многочлен вектора строки e^iT, а многочлен f_ij(s) определен соотношениями

, (1.22)

где p_i - степень многочлена d_i(s), d_ir+1(s), r = 0, ...p_i - 1 - его сопутствующие многочлены и

(1.23)

где i, j = 1,..., n; r = 0,..., p_i-1; e^iT0 = e^iT, A⁰ = I.

Значения вычисляются формальной заменой в силу определения 1.3. Заметим, что для многочленного вектора строки f^Tj(s) имеем неравенство (1.16). Значит для всякого корня l многочлена d_i(s) среди значений f_ij(l), j = 1, ..., n найдется хотя бы одно отличное от нуля, поскольку f_ij = (f^Ti)_j. Вернемся теперь к соотношениям (1.13) и заметим, что при

x(s) = R(s)x₀

будем иметь в силу соответствия (1.19)

(1.24)

Пусть j^j(s) вектор столбец многочленов, определенный по многочлену d_j(s) соотношениями

(1.25)

в силу соотношений (1.10), (1.4) при c = e^j = (0...1...0)^T с единичной j - той компонентой. Пусть d_j(s) минимальный многочлен вектора e^j и следовательно, d_j(A)e^j = 0.

Полагая в (1.13) v(s) = x₀ = e^j, c^T=e^iT получаем для "i,j" - го элемента изображения переходной матрицы

, (1.26)

где d_j(s) - минимальный многочлен вектора e^j, а многочлен j_ij(s) определен соотношениями

(1.27)

где p_j - степень многочлена d_j(s), d_jr+1(s), r = 0, ...p_j - 1 - его сопутствующие многочлены и

(1.23)

где i, j = 1,..., n; r = 0,..., p_j-1; e^j0 = e^j, A⁰ = I.

Значения вычисляются формальной заменой в силу определения 1.4.

Заметим, что для многочленного вектора (1.25) справедливо неравенство j^j(l) ¹ 0 (доказательство аналогично доказательству неравенства (1.17) для всякого корня l многочлена d_j(s). Значит среди значений j_ij(l), i = 1,..., n найдется хотя бы одно отличное от нуля, поскольку j_ij = e^iTj^j = (j^j)_i. Изложенное доказывет справедливость следующей теоремы.

Теорема 1.2

1. Пусть d_i(s), i = 1,..., n - минимальные многочлены вида векторов строк e^iT; i = 1,..., n соответственно, p_i, i = 1,..., n их степени, а d_ir(s), r = 1,...,p_i; i = 1,..., n - сопутствующие многочлены. Тогда для изображения переходной матрицы R(s) справедливо представление

(1.28)

где -многочленная матрица, компоненты которой определены соотношениями (1.22). Для всякого корня l минимального многочлена d_i(s), i = 1,..., n среди значений f_ij(l), j = 1,..., n найдется отличное от нуля.

2. Пусть d_j(s), j = 1,..., n - минимальные многочлены векторов e^j; j = 1,..., n соответственно, p_j, j = 1,..., n их степени, а d_jr(s), r = 1,...,p_j; j = 1,..., n - сопутствующие многочлены. Тогда для изображения переходной матрицы R(s) справедливо представление

(1.29)

где -многочленная матрица, компоненты которой определены соотношениями (1.27). Для всякого корня l минимального многочлена d_j(s), j = 1,..., n среди значений j_ij(l), i = 1,..., n найдется отличное от нуля.

1.1.5 Рассмотрим теперь реакцию системы на возмущающее воздействие, заданное в форме, принятой в теории управления для описания управляющих воздействий. Пусть сначала

.

Тогда

(1.30)

Последнее слагаемое в соотношениях (1.13) запишем в силу равенства (1.20)

(1.31)

Пусть d(s) - минимальный многочлен степени p вектора b с сопутствующими многочленами d_r(s), r = 1,..., p. Тогда из соотношения (1.13) получаем для реакции на выходе

(1.32)

где

(1.33)

причем векторный многочлен b(s) и многочлен d(s) взаимно просты. Пусть теперь

(1.34)

где B - m´n матрица со столбцами b^j Î Rⁿ, j =1,..., m. Пусть d_j(s) минимальный многочлен степени p_j вектора b^j, j =1,..., n. Записывая f(t) и y(t) соответственно в виде

(1.35)

где y_j(t) - реакция на воздействие , будем иметь с учетом соотношения (1.32)

(1.36)

где

(1.37)

причем векторные многочлены b^j(s) и многочлены d_j(s), j = 1,..., n соответственно взаимно просты. Равенства (1.37) в покомпонентной форме можно записать в виде

(1.38)

где i, j = 1,..., n; r = 0,..., p_j-1; b^j0 = b^j, A⁰ = I. Переходя к матричной форме записи соотношения (1.36), будем иметь на основании изложенного следующую теорему.

Теорема 1.3 Пусть d_j(s), j = 1,..., n - минимальные многочлены соответственно векторов b^j; j = 1,..., n - столбцов матрицы B, p_j, j = 1,..., n их степени, а d_jr(s), r = 1,..., p_j ; j = 1,..., n - сопутствующие многочлены. Для изображения реакции системы y(s) на воздействие (1.34) справедливо представление

где многочленная матрица b(s) определена равенством

со столбцами (1.37) и элементами (1.38).

Для всякого корня l многочлена d_j(s), j = 1,..., n среди значений b_ij(l), i =1,...,n найдется отличное от нуля.

1.1.6 Напомним теперь вычислительную процедуру построения минимального многочлена вектора. Рассмотрим последовательность векторов c, c¹ = Ac,..., c^k = Ac^k-1,... . Будем записывать в строчку их компоненты

вычисляя миноры образующейся матрицы при r = 2,3,... . Если на очередном шаге r < n среди миноров r + 1 - го порядка найдется хотя бы один отличный от нуля, то r + 1 строк матрицы линейно независимы, и следует переходить к следующему шагу r + 1. Когда в первый раз, скажем при r = p все миноры, p + 1- го порядка оказываются равными нулю (в силу конечно-мерности пространства p £ n ), имеем минимальную линейную комбинацию

. (1.39)

Для вычисления ее коэффициентов d₁,..., d_p заметим, что при r = p - 1 среди миноров p - го порядка записанной выше матрицы найдется хотя бы один отличный от нуля. Пусть i₁,...,i_p - номера столбцов этого минора. Тогда из равенства (1.38), записывая его в координатной форме, получаем систему уравнений

для коэффициентов d₁,..., d_p-1, d_p с неравным нулю определителем.

Таким образом, для вычисления коэффициентов минимального многочлена необходимы лишь вычисления числовых определителей, в чем и состоит основной эффект предложенного А.Н. Крыловым преобразования. Линейную комбинацию (1.39) можно построить и не прибегая к вычислению определителей. Для этого формируется последовательность векторов [1]

Числа выбираются из условия наращивания числа нулевых компонент векторов . Если на некотором шаге (r = p £ n ) в первый раз оказывается, что c^*p = 0, то тем самым и достигается построение линейной комбинации (1.39), т.к. векторы c^*r линейно зависимые от векторов . Имеем процесс типа процесса исключения Гаусса. При p = n имеем регулярный случай с результатом в виде характеристического определителя матрицы A. В общем случае указанными способами можно получить совокупность минимальных многочленов различных векторов, необходимую для представления заданного решения системы (1.1) в соответствии с предложенными теоремами. Изложенные методы построения изображений по Лапласу заданных решений, которые можно рассматривать как развитие метода А.Н. Крылова в форме, характерной для современной теории управления, предоставляют возможности анализа линейных стационарных систем, свободные от проблемы характеристического (векового) определителя системы.