1.1.1 Будем рассматривать линейную стационарную систему, заданную во временной области уравнениями состояния и выходов
где x(t)ÎRn вектор состояния, A - n´n заданная матрица коэффициентов, f(t) ÎRn – заданная вектор функция, cÎRn – вектор, определяющий выбор выхода системы y(t) )ÎR1. Традиционные подходы к построению заданного решения системы (1.1) так или иначе связаны с задачей обращения характеристической матрицы (sI – A). Например, преобразование Лапласа системы (1.1), сразу же алгебраизируя задачу, приводит в области изображений к соотношению
Формирование представления для обратной матрицы
где D(s) – характеристический многочлен, а P(s) – присоединенная (многочленная) матрица системы, представляет собою основную часть задачи. Последующее восстановление оригинала осуществляется уже сравнительно просто с помощью “техники” разложения изображения на простейшие дроби или теории вычетов ( и здесь рассматриваться не будет). Аналогичное место принадлежит задаче представления указанной обратной матрицы и в других подходах к построению заданного решения системы (1.1). Вычисление элементов этого представления выполняется либо с помощью миноров характеристической матрицы, включая характеристический определитель, либо методами типа Фаддеева – Леверрье. С повышением размерности системы сложность вычислений быстро возрастает. К тому же дело сильно осложняется при необходимости (например, в задачах анализа неасимптотической устойчивости) устранения общих нулей числителя и знаменателя представления, т.е. приведения его к виду
где P(s) - приведенная присоединенная матрица и D(s) – минимальный многочлен матрицы A взаимно просты [1]. Известно преобразование акад. А.Н. Крылова системы (1.1), которое существенно упрощает вычисление коэффициентов характеристического многочлена и алгебраическая интерпретация Ф.Р. Гантмахера этого преобразования [1] ( там же библиография по исследованию метода). В этой интерпретации характеристический многочлен в так называемом регулярном случае строится эффективным процессом исключения типа Гаусса как минимальный многочлен произвольно взятого вектора lÎRn. По существу, регулярный случай определен как такой, когда минимальный многочлен выбранного вектора совпадает с характеристическим. Если это не так ( степень минимального многочлена меньше степени n характеристического, и первый является лишь делителем второго), то метод не дает полного результата, поскольку не определена в общем виде роль минимальных многочленов векторов пространства Rn â конструкции заданного решения системы. В связи со сказанным описание этой роли представляется достаточно интересным и важным и является предметом нашего последующего изложения.
1.1.2 Напомним для удобства определения и отметим необходимые для дальнейшего свойства аннулирующих и минимальных многочленов [1]. Пусть рассматривается пространство состояний Rn системы с базисом e1,…, en.
Определение 1.1 Многочлен
называют аннулирующим многочленом матрицы A (аннулирующим многочленом пространства Rn относительно матрицы A), если
где I – единичная матрица. Многочлен минимальной степени в множестве аннулирующих многочленов матрицы A называют минимальным многочленом матрицы A.
Замечание 1.1 Характеристический многочлен
Определение 1.2 Пусть cÎRn и cr = Acr-1 = Arc, r = 1,…, p; c0 = c.
Условимся в обозначении
Многочлен (1.2) называют аннулирующим многочленом вектора c (относительно матрицы A), если d(c) = d(A)c = 0. Многочлен минимальной степени в множестве аннулирующих многочленов вектора c называют минимальными многочленами вектора c.
Определение 1.3 Пусть cTr = cTr-1A = cTAr, r = 1,…, p; cT0 = cT.
Условимся в обозначении
Многочлен (1.2) называют аннулирующим многочленом вектора cT (относительно матрицы A), если d(cT) = cTd(A) = 0. Многочлен минимальной степени в множестве аннулирующих многочленов вектора cT называют минимальными многочленами вектора cT.
Замечание 1.2 Аннулирующий многочлен d(s) вектора строки cT относительно матрицы A тождественно совпадает с таковым для вектора столбца c относительно матрицы AT, поскольку
Замечание 1.3 Пусть определены минимальные многочлены d1(s),…, dn(s) базисных векторов e1,…, en пространства Rn соответственно. Тогда их наименьшее общее кратное (НОК) является минимальным многочленом D(s) матрицы A
Замечание 1.4 Пусть d(s) минимальный многочлен какого-либо вектора строки или столбца. В ряду многочленов
всякий многочлен является делителем предшествующего.
Замечание 1.5 Аннулирующий многочлен матрицы A является в то же время и аннулирующим многочленом вектора cÎ Rn.
1.1.3 Построению модели заданного решения в области изображений предварим следующее
Утверждение 1.1 Для всякого многочлена
имеет место тождество
где
Тождество (1.10) проверяется перегруппировкой слагаемых. Многочлены (1.11) будем называть сопутствующими многочленами. Запишем уравнения состояния в изображениях по Лапласу
Далее с помощью этого соотношения найдем
Умножая уравнения в указанном порядке на 
Пусть d(s) – аннулирующий многочлен вектора строки cT , ò.å. cTd(A) = 0. Тогда из тождества (1.13) находим явное выражение для выхода системы
где векторный многочлен f(s) определен выражениями
в соответствии с обозначениями определения 1.2.
Замечание 1.6 В частности, в соответствии с замечаниями 1.5, 1.3 в соотношении (1.14) в качестве d(s) могут быть выбраны многочлены D(s), D(s) с соответствующим определением по соотношениям (1.15) многочлена fT(s).
Выбирая в качестве аннулирующего многочлена минимальный вектора строки cT, получаем следующую теорему.
Теорема 1.1 Пусть d(s) минимальный многочлен вида (1.2) вектора строки cT; dr(s), r = 1,..., p-1 - его сопутствующие многочлены. Тогда заданное решение системы (1.1) определяет ее выход в изображениях по Лапласу в виде (1.14), (1.15), где строка многочленов fT(s) и многочлен d(s) взаимно просты, т.е.
для всякого корня многочлена d(s).
Доказательство теоремы 1.1 В связи с изложенным остается доказать последнее утверждение. Оно следует из того, что
Действительно, нетривиальные многочлены d1(s),…, dp(s) при всяком s не обращаются одновременно в нуль (см. при m = p и равных нулю значениях многочленов систему (1.11) относительно коэффициентов d0 =1, d1,…, dp-1 с определителем, равным 1). Поэтому линейные комбинации в левой части неравенства также не могут обратиться в нуль в силу определения минимального многочлена (равенство повлекло бы за собою следствие о возможности построения минимального многочлена степени, меньшей чем p).
1.1.4 Пусть 
для изображения 
и
Последнее равенство легко усмотреть в силу экспоненциального представления переходной матрицы или, например, рассматривая матрицу
для которой домножением слева и справа на (sI - A) сразу находим X(s) = 0 для " s ¹ l, где l - корень характеристического многочлена det(sI-A) матрицы A. Из (1.18) следует, что "j" - столбца матрицы Ф(t) будем иметь уравнение (1.1) при f(t) = 0 и x0 = ej = (0...1...0)T с единичной j - той компонентой. Пусть fTj(s) вектор строка многочленов, определенных соотношением (1.15) при cT = eiT = (0...1...0)T с единичной i - той компонентой, и пусть fij(s), j = 1,..., n - компоненты этого вектора строки. Полагая в (1.14) v(s) = ej, cT = eiT, находим по соотношениям (1.14), (1.15) изображение i, j - го элемента переходной матрицы
где di(s) - минимальный многочлен вектора строки eiT, а многочлен fij(s) определен соотношениями
где pi - степень многочлена di(s), dir+1(s), r = 0, ...pi - 1 - его сопутствующие многочлены и
где i, j = 1,..., n; r = 0,..., pi-1; eiT0 = eiT, A0 = I.
Значения 
x(s) = R(s)x0
будем иметь в силу соответствия (1.19)
Пусть jj(s) вектор столбец многочленов, определенный по многочлену dj(s) соотношениями
в силу соотношений (1.10), (1.4) при c = ej = (0...1...0)T с единичной j - той компонентой. Пусть dj(s) минимальный многочлен вектора ej и следовательно, dj(A)ej = 0.
Полагая в (1.13) v(s) = x0 = ej, cT=eiT получаем для "i,j" - го элемента изображения переходной матрицы
где dj(s) - минимальный многочлен вектора ej, а многочлен jij(s) определен соотношениями
где pj - степень многочлена dj(s), djr+1(s), r = 0, ...pj - 1 - его сопутствующие многочлены и
где i, j = 1,..., n; r = 0,..., pj-1; ej0 = ej, A0 = I.
Значения 
![clip_image070[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgunemNVArM5djOFTuccqwl39aDVUvvdi2Iajl5hoRJaqirC3VAPb1pG3jIRuT1T13iTN1S5bOhUueHCZbW8GqInkj_62zydJN4YewCUCt5hVuXv1ZtEyhpb-y_TEbPS3iQj4flFOyS2pA/s1600-h/clip_image070%25255B1%25255D%25255B2%25255D.gif "clip_image070[1]"){kind=small}
Заметим, что для многочленного вектора (1.25) справедливо неравенство jj(l) ¹ 0 (доказательство аналогично доказательству неравенства (1.17) для всякого корня l многочлена dj(s). Значит среди значений jij(l), i = 1,..., n найдется хотя бы одно отличное от нуля, поскольку jij = eiTjj = (jj)i. Изложенное доказывет справедливость следующей теоремы.
Теорема 1.2
1. Пусть di(s), i = 1,..., n - минимальные многочлены вида векторов строк eiT; i = 1,..., n соответственно, pi, i = 1,..., n их степени, а dir(s), r = 1,...,pi; i = 1,..., n - сопутствующие многочлены. Тогда для изображения переходной матрицы R(s) справедливо представление
где 
2. Пусть dj(s), j = 1,..., n - минимальные многочлены векторов ej; j = 1,..., n соответственно, pj, j = 1,..., n их степени, а djr(s), r = 1,...,pj; j = 1,..., n - сопутствующие многочлены. Тогда для изображения переходной матрицы R(s) справедливо представление
где 
1.1.5 Рассмотрим теперь реакцию системы на возмущающее воздействие, заданное в форме, принятой в теории управления для описания управляющих воздействий. Пусть сначала
Тогда
Последнее слагаемое в соотношениях (1.13) запишем в силу равенства (1.20)
Пусть d(s) - минимальный многочлен степени p вектора b с сопутствующими многочленами dr(s), r = 1,..., p. Тогда из соотношения (1.13) получаем для реакции на выходе
где
причем векторный многочлен b(s) и многочлен d(s) взаимно просты. Пусть теперь
где B - m´n матрица со столбцами bj Î Rn, j =1,..., m. Пусть dj(s) минимальный многочлен степени pj вектора bj, j =1,..., n. Записывая f(t) и y(t) соответственно в виде
где yj(t) - реакция на воздействие 
где
причем векторные многочлены bj(s) и многочлены dj(s), j = 1,..., n соответственно взаимно просты. Равенства (1.37) в покомпонентной форме можно записать в виде
где i, j = 1,..., n; r = 0,..., pj-1; bj0 = bj, A0 = I. Переходя к матричной форме записи соотношения (1.36), будем иметь на основании изложенного следующую теорему.
Теорема 1.3 Пусть dj(s), j = 1,..., n - минимальные многочлены соответственно векторов bj; j = 1,..., n - столбцов матрицы B, pj, j = 1,..., n их степени, а djr(s), r = 1,..., pj ; j = 1,..., n - сопутствующие многочлены. Для изображения реакции системы y(s) на воздействие (1.34) справедливо представление
где многочленная матрица b(s) определена равенством
со столбцами (1.37) и элементами (1.38).
Для всякого корня l многочлена dj(s), j = 1,..., n среди значений bij(l), i =1,...,n найдется отличное от нуля.
1.1.6 Напомним теперь вычислительную процедуру построения минимального многочлена вектора. Рассмотрим последовательность векторов c, c1 = Ac,..., ck = Ack-1,... . Будем записывать в строчку их компоненты
вычисляя миноры образующейся матрицы при r = 2,3,... . Если на очередном шаге r < n среди миноров r + 1 - го порядка найдется хотя бы один отличный от нуля, то r + 1 строк матрицы линейно независимы, и следует переходить к следующему шагу r + 1. Когда в первый раз, скажем при r = p все миноры, p + 1- го порядка оказываются равными нулю (в силу конечно-мерности пространства p £ n ), имеем минимальную линейную комбинацию
Для вычисления ее коэффициентов d1,..., dp заметим, что при r = p - 1 среди миноров p - го порядка записанной выше матрицы найдется хотя бы один отличный от нуля. Пусть i1,...,ip - номера столбцов этого минора. Тогда из равенства (1.38), записывая его в координатной форме, получаем систему уравнений
для коэффициентов d1,..., dp-1, dp с неравным нулю определителем.
Таким образом, для вычисления коэффициентов минимального многочлена необходимы лишь вычисления числовых определителей, в чем и состоит основной эффект предложенного А.Н. Крыловым преобразования. Линейную комбинацию (1.39) можно построить и не прибегая к вычислению определителей. Для этого формируется последовательность векторов [1]
Числа 
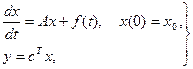
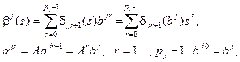
0 коммент.:
Отправить комментарий