Общие теоретические сведения.
Математическая модель САУ обычно записывается в форме векторного дифференциального уравнения, где свойства системы неявно выражены коэффициентами некоторых матриц. Эта форма записи является традиционной и предназначена для применения математического аппарата ТАУ. Получение матриц, характеризующих объекты реального мира, является задачей по сложности не уступающей, а по материальным затратам иногда превосходящей исследование уже готовой математической модели. Поэтому, перед тем как начать исследование математической модели реального летательного аппарата (ЛА) приведем общее описание пути построения ее самой.
Движение ЛА происходит под действием аэродинамических сил и моментов, сил и моментов двигателей и гравитационных сил. При определении движения ЛА необходимо в общем случае решить следующие задачи:
найти угловые и линейные скорости ЛА, обусловленные действием на него перечисленных сил и моментов;
определить углы ориентации ЛА относительно набегающего на него потока и осей координат , связанных с Землей;
определить перемещение самолета относительно Земли.
Обычно считается, что ЛА представляет собой абсолютно жесткое тело, масса и моменты инерции которого на рассматриваемых интервалах времени неизменны. Конфигурация ЛА имеет плоскость симметрии и массы распределены симметрично по отношению к этой плоскости. Используются следующие прямоугольные системы координат(рис.)
Нормальная земная система координат OXgYgZg. Эта система осей координат имеет неизменную ориентацию относительно Земли.
Начало координат совпадает с центром масс ЛА. Оси OXg и ОZg лежат в горизонтальной плоскости, ось OYg направлена вверх по местной вертикали.
Связанная система координат OXYZ. Начало координат расположено в центре масс ЛА. Ось ОХ лежит в плоскости симметрии и направлена вдоль линии хорд крыла к носовой части ЛА. Ось ОY лежит в плоскости симметрии самолета и направлена вверх (при горизонтальном полете), ось OZ дополняет систему до правой.
Положение связанной системы осей координат OXYZ относительно нормальной земной системы координат OXgYgZg может быть полностью определено так называемыми углами Эйлера (рис.2):
· угол рыскания y,
· угол тангажа J,
· угол крена g.
Последовательно поворачивая связанную систему на каждый из углов Эйлера, можно прийти к любому угловому положению связанной системы относительно осей нормальной системы. Положение связанной системы относительно вектора скорости центра масс ЛА определяется углами :
-атаки a,
-скольжения b.
При выходе уравнений движения ЛА необходимо рассматривать векторные уравнения изменения количества движения (движения ц.м.) и момента количества движения (вращения вокруг ц.м.), законы сложения линейных и угловых скоростей и выражения для сил и моментов. Ниже приводятся все уравнения движения ЛА, составляющие замкнутую систему уравнений.
1) Уравнения движения центра масс (уравнения поступательного, линейного движения; уравнения сил):
где - вектор скорости вращения связанных с ЛА осей;
- главный вектор аэродинамических сил.
Символом обозначена полная производная (производная в земной системе), символом
- местная производная (в связанной системе),
- любой вектор.
Тогда уравнения перемещения в проекциях на связанные оси запишутся так:
2) Уравнения вращения вокруг центра масс (уравнения вращательного, углового движения; уравнения моментов):
где - момент количества движения;
Т - тензор инерции ЛА относительно связанных осей;
Jx,y,z - моменты инерции.
Уравнение вращения в проекциях на связанные оси будут иметь вид:
3) Закон сложения угловых скоростей:
Отсюда:
и
4) Закон сложения линейных скоростей:
5) Проекции скорости на связанные оси:
6) Проекции сил на связанные оси.
Проекции силы тяжести:
Проекции силы тяги двигателя:
Проекции аэродинамической силы:
7) Проекция момента сил на связанные оси:
8) Безразмерные коэффициенты аэродинамических сил и моментов:
Проведя линеаризацию этих уравнений, получим две системы плоскостных движений.
Уравнения продольного движения:
Уравнения бокового движения:
Требуется рассчитать переходный процесс для модели бокового движения тяжелого самолета «Боинг - 747» в посадочной конфигурации. Его линеаризованная модель движения в конфигурации , используемой при посадке , без применения системы автоматического повышения устойчивости имеет вид :
Здесь приняты следующие обозначения для фазовых переменных :
u - скорость бокового скольжения ;
wY - угловая скорость рыскания ;
wX - угловая скорость крена ;
g - угол крена ;
y - угол рыскания ;
Z - боковое отклонение .
Управлениями в системе являются :
dЭ - угол отклонения элеронов ;
dН - угол отклонения руля направления .
Возмущением в системе является ветер :
v - скорость ветра .
Уравнения записаны в безразмерных величинах. В качестве единицы для углов принято 0.01 рад, а для скоростей - 0.305 м/с.
Для удобства построения характеристик, которые будут рассматриваться далее, приведем уравнения , описывающие данную модель , в матричной форме :
где
Вектор фазовых переменных обозначим через x ;
Управление организовано в виде обратной связи
Достоинством такого подхода к построению управления является хорошая согласованность движений по различным каналам .





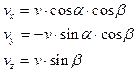


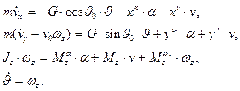






0 коммент.:
Отправить комментарий