ВЫЧИСЛЕНИЕ ИНФОРМАЦИОННЫХ ПОТЕРЬ ПРИ ПЕРЕДАЧЕ СООБЩЕНИЙ ПО КАНАЛАМ СВЯЗИ С ШУМАМИ

 

Потери информации в каналах связи с шумами обычно описывают при помощи условной энтропии и энтропии объединения.

Если помех нет или их уровень настолько низок, что они и в состоянии уничтожить сигнал или имитировать полезный сигнал в отсутствие передачи, то при передаче а_i мы будем твердо уверены, что получим b_j – сигнал, соответствующий переданному a_i сигналу. События А и В статически жестко связаны, условная вероятность максимальна , а условная энтропия

, (23)

так как . В этом случае количество информации, содержащейся в принятом ансамбле сообщений В, равно энтропии передаваемых сообщений ансамбля А, т. е. 1.

При высоком уровне помех любой из принятых сигналов b_j может соответствовать любому переданному сигналу а_i, статистическая связь между переданными и принятыми сигналами отсутствует.

В этом случае вероятности и есть вероятности независимых событий и .

,

так как , т. е. Условная энтропия равна безусловной, а количество информации, содержащееся в В, относительно А равно нулю:

.

Информационные характеристики реальных каналов связи лежат между этими двумя предельными случаями. При этом потери информации при передаче k символов по данному каналу связи

.

Несмотря на то, что часть информации поражается помехами, между принятыми сообщениями существует статистическая взаимосвязь. Это позволяет описывать информационные характеристики реальных каналов связи при помощи энтропии объединения статистически зависимых событий. Так как

. (24)

то потери в канале связи могут быть учтены при помощи энтропии объединения следующим образом:

, (25)

а с использованием условной энтропии:

.

Для вычисления среднего количества информации, содержащегося в принятом ансамбле сообщений B относительно переданного ансамбля сообщений А в условиях действия помех, пользуются следующими выражениями, выведенными непосредственно из выражения (25):

, (26)

, (27)

. (28)

Для вычислений число удобно применять выражения (26-28) в виде:

,

,

.

Для полного и всестороннего описания канала связи необходимо задать: канальную матрицу вида и безусловные вероятности вида или канальную матрицу вида и безусловные вероятности вида , или канальную матрицу вида . В последнем случае сумма значений матрицы по столбцам дает безусловные

вероятности вида , а сумма по строкам даёт безусловные вероятности вида 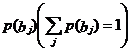. Условные вероятности могут быть найдены из выражений:

.

Зная условные и безусловные вероятности, можно найти H(A),H(B),H(A/B) и H(B/A).

Если уровень помех настолько высок, что с равной вероятностью можно ожидать переход любого символа источника сообщения в произвольный символ первичного алфавита, то энтропия канала связи будет равна , а количество информации I=H(A)-, при этом значении I может быть отрицательной величиной, что означает, что канал связи вносит дезинформацию.

---

1 При повторных (многократных) передачах .

Предлагаю ознакомиться с аналогичными статьями: