Понятие условной энтропии в теории информации используется при определении взаимозависимости1между символами кодируемого алфавита, для определения потерь при передаче информации по каналам связи, при вычислении энтропии объединения.
Во всех случаях при вычислении условной энтропии в том или ином виде используются условные вероятности.
Если при передаче n сообщений символ А появился m раз, символ B появился l раз, а символ А вместе с символом В - раз, то вероятность появления символа А
вероятность появления символа В
; вероятность совместного появления А и В
условная вероятность появления символа А относительно символа В и условная вероятность появления символа В относительно символа А
Если известна условная вероятность, то можно легко определить и вероятность совместного появления символов А и В, используя выражение (7)
От классического выражения (4) формула условной энтропии отличается тем, что в ней вероятности – условные:
где индекс i выбран для характеристики произвольного состояния источника сообщений А, индекс j выбран для характеристики произвольного состояния адресата В.
Различают понятия частной и общей условной энтропии. Выражения (9) и (10) предоставляют собой частные условные энтропии.
Общая условная энтропия сообщения В относительно сообщения А характеризует количество информации, содержащейся в любом символе алфавита, и определяется усреднением по всем символам, т.е. по всем состояниям с учетом вероятности появления каждого из состояний, и равна сумме вероятностей появления символов алфавита на неопределённость, которая остаётся после того, как адресат принял сигнал
Выражение (11) является общим выражением для определения количества информации на один символ сообщения для случая неравномерных и взаимозависимых символов.
Так как представляет собой вероятность совместного появления двух событий
то формулу (11) можно записать следующим образом:
Понятие общей и частной условной энтропии широко используется при вычислении информационных потерь в каналах связи с шумами.
В общем случае, если мы передаём m сигналов А и ожидаем получить m сигналов В, влияние помех в канале связи полностью описывается канальной матрицей, которую мы приводим ниже:
| В А | b1 | b2 | … | bj | … | bm |
| a1 | …, | …, | ||||
| a2 | …, | …, | ||||
| … | ………...… | ………...… | ………...… | ………...… | ………...… | ………...… |
| ai | …, | …, | ||||
| … | ………...… | ………...… | …, | ………...… | …, | ………...… |
| am | …, | …, |
Вероятности, которые расположены по диагонали (выделенные полужирным шрифтом), определяют правильный приём, остальные – ложный. Значение цифр, заполняющих колонки канальной матрицы, обычно уменьшается по мере удаления от главной диагонали и при полном отсутствии помех все, кроме цифр, расположенных на главной диагонали, равны нулю.
Если описывать канал связи со стороны источника сообщений, то прохождение данного вида сигнала в данном канале связи описывается распределением условных вероятностей вида так для сигнала ai распределением вида
Сумма вероятностей распределения (13) всегда должна равняться 1. Потери информации, которые приходятся на долю сигнала a1, описываются при помощи частной условной энтропии вида
Суммирование производиться по j, так как i-е cсостояние (в данном случае первое) остаётся постоянным.
Чтобы учесть потери при передаче всех сигналов по данному каналу связи, следует просуммировать все частные условные энтропии, т.е. произвести двойное суммирование по i и по j. При этом в случае равновероятных появлений сигналов на выходе источника сообщений
(на m делим, так как энтропия есть неопределённость на один символ).
В случае неравновероятного появления символов источника сообщений следует учесть вероятность появления каждого символа, умножив на неё соответствующую частную условную энтропию. При этом общая условная энтропия
Если мы исследуем канал связи со стороны приёмника сообщений, то с получением сигнала bj предполагаем, что был послан какой-то из сигналов a1,a2,…,ai,…,am. При этом канальная матрица будет иметь вид
| В А | b1 | b2 | … | bj | … | bm |
| a1 | …, | …, | ||||
| a2 | …, | …, | ||||
| … | ………...… | ………...… | ………...… | ………...… | ………...… | ………...… |
| ai | …, | …, | ||||
| … | ………...… | ………...… | …, | …, | ………...… | |
| am | …, | …, |
В этом случае единице должны равняться суммы условных вероятностей не по строкам, а по столбцам канальной матрицы
Частная условная энтропия
а общая условная энтропия
Так как то для вычисления общей условной энтропии наравне с выражением (16) может быть использовано следующее выражение:
Если заданы канальная матрица вида (частная условная энтропия в этом случае соответствует (14) и безусловные вероятности вида
, то безусловные вероятности приемника
находим как
т. е. Если заданы безусловные вероятности источника и канальная матрица, то может быть вычислена энтропия приёмника
и наоборот, если заданы вероятности вида и канальная матрица, описывающая канал связи со стороны приемника сообщений
(частная условная энтропия при этом соответствует выражению (17)), то а значит может быть определена энтропия источника сообщений
Если взаимозависимость связывает 3 элемента ai, aj, ak, то условная энтропия вычисляется по формуле
аналогично и для 4, 5, …, n элементов.
Энтропия объединения используется для вычисления энтропии совместного появления статистически зависимых сообщений. Например, передав сто раз цифру 5 по каналу связи с помехами, заметим, что цифра 5 была принята 90 раз, цифра 6 – 8 раз и цифра 4 – 2 раза.
Неопределённость возникновения комбинаций вида 5 – 4, 5 – 5, 5 – 6, при передаче цифры 5 может быть описана при помощи энтропии объединения. H(A,B) – неопределенность того, что будет послано А, а принято В. Для ансамблей переданных сообщений и принятых сообщений В энтропия объединения представляет собой сумму вида
Энтропия объединения и условная энтропия связаны между собой следующими соотношениями:
Энтропия объединения может быть подсчитана при помощи матрицы вида
Такая матрица обладает замечательным свойством: при этом
. Это свойство, в свою очередь, позволяет вычислять энтропию - как источника, так и приёмника сообщений непосредственно по канальной матрице
Суммирование производим по i и j, так как для того, чтобы найти безусловные вероятности, необходимо суммировать их по одной координате (имея в виду матричное представление вероятностей) для нахождения Н суммирование производится по другой координате.
Условные вероятности вида и
вычисляются следующим образом:
Количество информации на символ сообщения, переданного по каналу связи, в котором влияние помех описывается при помощи энтропии объединения, подсчитывается следующим образом:
Контрольные задачи
1.В результате статистических испытаний канала связи № 1 со стороны источника сообщений были получены следующие условные вероятности: 0,9;
0,1;
0;
0,1;
0,8;
0,1;
0;
0;
0,9.
При испытании канала связи № 2 со стороны приёмника сообщений получины условные вероятности: 0,9;
0,08;
0;
0,1;
0,8;
0,0;
0;
0,12;
0,92.
Построить соответствующие канальные матрицы и определить частные условные энтропии относительно сигнала а2 (со стороны источника сообщений) и сигнала b3( со стороны приёмника).
2.Определить все возможные информационные характеристики канала связи, в котором взаимосвязь источника с приёмником может быть описана матрицей вида:
3.Вероятности появления сигналов на входе приемника сообщений равны соответственно: p(b1) = 0,2; p(b2) = 0,3; p(b3) = 0,3. Канал связи описан следующей канальной матрицей:
Определить энтропию источника сообщений.
4.Определить частотную энтропию относительно каждого символа источника сообщений при передаче по каналу связи, описанному следующей канальной матрицей:
5.В результате статистических испытаний канала связи были получены следующие условные вероятности перехода одного сигнала в другой : 0,85;
0,1;
0,05;
0,09;
0,91;
0;
0;
0,08;
0,92. Построить канальную матрицу и определить общую условную энтропию сообщений, передаваемых по данному каналу связи.
6.Построить произвольные канальные матрицы, описывающие канал связи как со стороны источника сообщений, так и со стороны приёмника. В чём разница таких матриц? Как определить частные условные энтропии по одной и по другой матрице?
7.Построить произвольную матрицу некоторой объединенной системы. Какие замечательные свойства такой матрицы?
8.Показать процесс перехода от матрицы с вероятностями вида p(a,b) к матрице с вероятностями вида p(b/a).
9.Определить полные условные энтропии двух систем А и В, если матрица вероятностей системы, полученной в результате объединения систем А и В, имеет вид:
1 Суть взаимозависимости символов букв алфавита заключается в том, что вероятность появления i-й буквы в любом месте сообщения зависит от того, какие буквы стоят перед ней и после неё, и будет отличаться от безусловной вероятности pi, известной из статистических свойств данного алфавита.

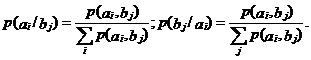




0 коммент.:
Отправить комментарий