Как уже указывалось, применение методов теории вероятностей при однократной реализации исхода принятого решения, вообще говоря, неправомерно. Методологически близкая ситуация возникает и в случаях многократной реализации исхода, но при дополнительном предположении, что либо распределение вероятностей параметра z неизвестно, либо параметр неопределенности z изменяется неизвестным образом, но не является случайным (не обладает свойством статистической устойчивости - так называемый случай полной неопределенности) [6,10].
В указанных ситуациях информация о факторе неопределенности обычно имеет вид
где Z - некоторое множество. Но подобной информации также недостаточно для однозначного решения задачи выбора альтернативы x.
Напомним, что мы попрежнему рассматриваем задачу оптимизации I(x,z). Из решения этой задачи мы можем определить вектор x как функцию z:
x=x(z). (7)
Формула (7) позволяет лишь отобразить множество неопределенности природных факторов Z на множестве GxX, которое естественно назвать множеством неопределенности решений x. Выбор конкретного элемента из множества Gx может основываться на введении различных разумных гипотез о поведении cреды. Одна из важнейших гипотез такого типа называется гипотезой антагонизма. Она состоит в предположении, что среда ведет себя “наихудшим” (для принимающего решение) образом. В итоге в качестве оптимальной альтернативы выбирается решение задачи оптимизации :
Из последнего соотношения видно, что для вычисления значения функционала I4(x) при фиксированном значении x решается задача минимизации I(x,z) по z, т.е. подбирается “наихудший” возможный вариант z. Соответствующее значение I берется в качестве значения функционала I4, соответствующего заданному x. Принцип выбора оптимальной альтернативы x* на основе решения задачи (8) называется также принципом гарантированного результата или принципом максимина. Число I4(x*)=I* называется гарантированной оценкой, а сам элемент x* - гарантирующим решением. Смысл введенных названий состоит в том, что, каково бы ни было значение параметра неопределенности z, выбор x=x* согласно формуле (8) гарантирует, что при любом z значение целевого функционала I(x,z) будет не меньше, чем I* (докажите последнее замечание).
Пример 1.6.
Для примера 3 из введения гипотеза антагонизма формулируется в виде следующего предположения: если студент не берет билет, контролер появляется. Показателем “полезности” первой альтернативы x1 (брать билет) является ее гарантированный уровень: I4(x1)=min{-40,-40}=-40 ( Таблица 6). Для второй альтернативы I4(x2)=min{-840,0}=-840. Наибольший из гарантированных результатов (максимин) равен (-40), а альтернатива x1 (брать билет) является в указанном смысле оптимальной: x*=x1.
Очевидно, что если значение функционала I(x,z) отражает не “ полезность” альтернативы x, не “доход”, а, напротив, - “потери”, то исходная задача состоит в минимизации функции I(x,z), а максиминный критерий превращается в минимаксный:
Максиминный (минимаксный) критерий является крайне осторожным, “пессимистичным”, что может иногда приводить к нелогичным выводам, противоречащим здравому смыслу.
Пример 1.7.
Пусть функция I(x,z) задана с помощью таблицы 8, где элементы матрицы имеют смысл “потерь”, которые следует минимизировать.
Таблица 8
| Z X | z1 | z2 |
| x1 | 10100грн. | 100грн. |
| x2 | 10000грн. | 10000грн. |
При выборе решения x1 или x2 мы по-прежнему не знаем, какое значение z1 или z2 примет фактор неопределенности z. Применение минимаксного критерия приводит к выбору x2. Но интуитивно мы должны выбрать x1, поскольку совсем не исключено, что реализуется “состояние природы” z2 и наш проигрыш будет существенно уменьшен (равен 100 грн.). В то же время при выборе x2 мы гарантировано получим потери в 10000 грн. при любом значении z.
Предположим теперь, что задана таблица 9, представляющая функционал I(x,z).
Таблица 9
| Z X | z1 | z2 | zm | |
Здесь введены обозначения I(xi,zj). Таким образом, мы предполагаем конечность множеств X,Z. Поясним на этом примере, как можно исправить положение с излишней “осторожностью” максиминного (или минимаксного) критерия.
Вместо матрицы {} введем матрицу
, элемент
которой определяется согласно (10). Иначе говоря, rij есть разность между наилучшим значением в столбце j и значением
при том же j. Обработка матрицы {
} идет “по столбцам”.
Построенная таким способом матрица {rij} называется матрицей сожаления, так как, по существу, каждое число rij выражает “сожаление” лица, принимающего решение, по поводу того, что он не выбрал наилучшего решения относительно состояния zj [7,11].
Критерий минимального сожаления, предложенный Сэвиджем, состоит в применении минимаксного критерия (независимо от того, какой характер имели элементы - “дохода” или “потерь”) к матрице сожаления {rij};
т.е. числа rij всегда носят характер “потерь” и их необходимо минимизировать.
Обратимся снова к последнему примеру. Матрица сожалений будет иметь вид таблицы 10
Таблица 10
| Z X | z1 | z2 |
| x1 | 100грн. | 0грн. |
| x2 | 0грн. | 9900грн. |
В этом случае имеем:
В результате, согласно критерию Сэвиджа, выбираем первую альтернативу x1, к чему мы и стремились интуитивно.
Следующий критерий оптимальности принимаемого решения называется критерием Гурвица. Этот критерий охватывает ряд различных подходов к принятию решения: от наиболее оптимистичного до наиболее пессимистичного [7,11].
Наиболее оптимистичный подход (в предположении, что означает “ выигрыш” или “доход”) состоит в выборе x* из условия
Аналогично при наиболее пессимистичных предположениях выбираемое решение соответствует
Критерий Гурвица (называется также критерием пессимизма – оптимизма) сводится к взвешенной комбинации обоих способов, устанавливая баланс между случаями крайнего оптимизма и крайнего пессимизма. Если означает “прибыль”(т.е. соответствующие величины необходимо максимизировать), то выбирается решение из условия
В том случае, когда представляет “затраты”, оптимальное решение удовлетворяет аналогичному соотношению :
При =1 имеем случай крайнего оптимизма (11); при
=0 - случай крайнего пессимизма (12). Промежуточные значения показателя пессимизма - оптимизма
характеризуют ту или иную склонность лица, принимающего решение, к пессимизму или оптимизму. При отсутствии явно выраженной склонности целесообразно полагать
=1/2.
В непрерывном случае, когда аргументы функционала I(x,z) не обязаны принадлежать конечным множествам, имеем
или
Aналогично для критерия Сэвиджа :
где (в предположении, что функционал I требуется максимизировать)
Пример 1.8.
Один из кооперативов, занимающийся обслуживанием населения, должен определить уровень предложения услуг так, чтобы удовлетворить потребности клиентов в течение предстоящих праздников. Точное число клиентов неизвестно, но ожидается, что оно может принять одно из четырех значений: z1=200, z2=250, z3=300, z4=350. Для каждого из этих возможных значений zj существует наилучший уровень предложения (с точки зрения возможных затрат). Отклонения от этих уровней приводят к дополнительным затратам либо из-за превышения предложения над спросом, либо из-за неполного удовлетворения спроса.
Затраты I (в тыс. грн.) приведены в таблице 11, где xi означают варианты уровней предложения, среди которых надлежит найти оптимальный (значения функционала I в данном примере имеют смысл «потерь»).
Таблица 11
| Z X | z1 | z2 | z3 | z4 |
| x1 | 5 | 10 | 18 | 25 |
| x2 | 8 | 7 | 8 | 23 |
| x3 | 21 | 18 | 12 | 21 |
| x4 | 30 | 22 | 19 | 15 |
Заметим, что все отраженные в таблице11 уровни предложения оказываются наилучшими для соответствующих значений zj. Так, x1 оказывается наилучшим при z = z1, x2 - при z = z2, x3- при z = z3 и x4- при z = z4. Таким образом “лишних “ xi в таблице 11 не содержится. Применение минимаксного критерия к выбору решения позволяет вычислить гарантированное значение I* = 21 и x* = x3. Критерий Сэвиджа приводит к матрице сожаления (13).
В результате минимаксной обработки матрицы R получаем x*=x2, что соответствует “сожалению”, равному 8.
Критерий Гурвица при a=1/2 приводит к выбору решения x*=x1 или x*= x2. Необходимые промежуточные результаты представлены в таблице12.
Таблица 12
| X | Примечание | |||
| x1 | 5 | 25 | 15 | |
| x2 | 7 | 23 | 15 | min |
| x3 | 12 | 21 | 16,5 | |
| x4 | 15 | 30 | 22,5 |
Упражнения.
а). Примените минимаксный критерий в приведенном примере, если четвертое значение возможного числа клиентов z4 исключено. Ответ: минимаксное значение равно 8 и соответствует решению x2.
б). Примените критерий Сэвиджа, предполагая, что решение x2 исключено. Ответ: минимаксное значение rij = 10 и соответствует выбору x1.
в). Решите этот пример с помощью критерия Гурвица при a=0.75.
Ответ: cледует выбрать x1 со значением целевой функции 10.

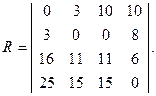
0 коммент.:
Отправить комментарий