Проблемы эквивалентности и распознавания принадлежности к некоторому классу алгоритмов в своей полной подстановке являются алгоритмически неразрешимыми проблемами. До сих пор их решали только для некоторых видов алгоритмических систем при довольно узком определении эквивалентности.
Основные результаты относятся к операторным схемам.
В качестве характерных черт операторных схем можно выделить следующие черты:
-совокупность операторов, образующих схему алгоритма, изображается явно;
-для каждого оператора явно указываются его приемники и предшественники по выполнению, а также его аргументы и результаты;
-при построении реализации приемник оператора обычно выбирается без учета истории движения к этому оператору;
-если в рассмотрение вовлекается некоторая величина, «вырабатывается» некоторым оператором, то она трактуется как независимая переменная, то есть считается, что после выполнения данного оператора она может принимать любое значение независимо от предыдущей истории;
-если аргументом или результатом оператора оказывается компонента массива, указанная индексом, то значение индекса обычно игнорируется и считается, что аргументом и результатом оператора является весь массив.
Первой работой, посвященной общей теории преобразования алгоритмов, явилась работа Ю.И. Янова «О логических схемах алгоритмов». В ней были сформулированы основные компоненты теории преобразования алгоритмов, а именно:
-формализация понятия схемы алгоритма;
-задание отношения эквивалентности;
-определение алгоритма, распознающего эквивалентность схем;
-построение системы преобразований, полной в том смысле, что любую пару эквивалентных алгоритмов можно трансформировать один в другой последовательным применением этих преобразований, сохраняющих эквивалентность.
Всякий алгоритм при переработке конкретного объекта предписывает однозначно определенную последовательность элементарных действий. Такая последовательность, вообще говоря, различна для различных объектов, к которым данный алгоритм может быть применен. Однако всегда найдется конечное множество предикатов, характеризующих некоторые свойства перерабатываемых объектов, такое, что для данного алгоритма зависимость порядка выполнения элементарных действий от перерабатываемых объектов будет однозначной функцией этих предикатов.
Такая функция может быть записана при помощи конечной строки, составленной из символов элементарных действий А1,A2,…,An( называемых операторами), предикатов и некоторых вспомогательных символов: [i ; i] (i=1.2….), называемых соответственно левой и правой полускобками.
Строка А1А2А3…Аs означает, что последовательно должны быть выполнены операторы А1 ,А2, А3, …,Аs.
Строка А1 р[iA2…i]A3 ,
где р - некоторый предикат, означает, что после выполнения оператора А1 в случае р=1 должен быть выполнен оператор А2 ,стоящий непосредственно правее р[i, а если р=0, то оператор А3, стоящий справа от полускобки i].
Строки такого вида называются схемными записями алгоритмов. Один и тот же алгоритм при фиксированном множестве элементарных операций и предикатов может иметь различные логические схемы.
Рассмотрим пример схемной записи нормального алгоритма:
…………..;
Ps à .Qs;
………….;
Pn à Qn ,
где Ps à . Qs является заключительной подстановкой.
Обозначим через Pi предикат «слово Pi входит в перерабатываемое слово», а через Ai – операцию замены первого вхождения слова Pi в перерабатываемое слово Qi (i=1,2,…,n).
Тогда строка
___|…_____| _____| …____| P1 |__ A10|____ __| P2 |__ А20|___ …__| Ps
n+1 n+s-1 n+s-1 2n 1 n+1 1 2 n+2 s-1
|__As0|___…___|Pn|__An0 |__ _| ___|
s n+s n-1 n 2n n n+s
есть схемная запись рассматриваемого нормального алгоритма.
«0» здесь означает тождественно ложный предикат.
Очевидно, что для всякого слова R в алфавите А последовательность
Ai1, Ai2, …,( 1<=is<=n, s=1,2,…) над этим словом, которую предписывает схемная запись совпадает с последовательностью тех преобразований слова R , которая возникает при применении к нему нормального алгоритма.
Если в схемных записях алгоритмов отвлечься от содержательного смысла операторов, считая их элементарными символами, а предикаты соответственно независимыми логическими переменными, то полученные выражения будем называть логическими схемами алгоритмов (ЛСА).
Один и тот же алгоритм при фиксированном множестве операций и предикатов может иметь различные логические схемы.
Например, выражения:
__
P1\/P2|__ __| A1 P2 |__ 0|__ __| A2 __|
1 2 2 3 1 3
__
P1/\P2|__ A20|__ __| ___| A1 P2 |___ __|
1 2 1 3 3 2
являются схемными записями одного и того же алгоритма.
Будем считать, что значения логических переменных могут изменяться только в моменты выполнения операторов. При этом, поскольку в логических схемах алгоритмов не содержится никакой информации о поведении значений логических переменных, то некоторые ограничения на возможности их изменения будем задавать извне с помощью распределений сдвигов, то есть соответствий между операторами и множествами логических переменных.
Если задано какое-либо распределение сдвигов Аi-Pi,
где Аi - операторы, Рi - множество логических переменных (i=1,2,…, ), то будем считать, что в момент выполнения оператора Аi могут изменяться значения только тех логических переменных, которые входят в Pi.
Пусть для некоторой схемы задана последовательность D1,D2,…,Ds… наборов значений логических переменных. Если считать, что при выполнении схемы они изменяются согласно этой последовательности, то есть после выполнения s-того оператора логические переменные принимают набор значений Ds, то получим определенную последовательность выполненных операторов, которую будем называть значением схемы для данной последовательности наборов.
Задание распределения сдвигов выделяет для каждой схемы из всех возможных последовательностей наборов множество допустимых последовательностей.
Понятие эквивалентности схем при заданном распределении сдвигов требует совпадения значений эквивалентных схем для любой допустимой последовательности наборов.
Это означает, что множество всех эквивалентных схем при любой подстановке конкретных операторов и предикатов переходит во множество схемных записей одного и того же алгоритма.
Ю. И. Яновым и А. П. Ершовым была введена система аксиом и правил вывода, описывающая понятие эквивалентности логических схем алгоритмов при данном распределении сдвигов. В них оператор рассматривается как система функций, берущих свои аргументы из некоторых входных величин и записывающих результаты в выходные величины оператора.
Операторной схемой Янова называется конечный ориентированный граф, обладающий следующими свойствами:
-вершины графа имеют не более двух выходящих из них стрелок;
-вершины, из которых выходят по две стрелки (одна из которых помечается), называются распознавателями;
-к одной из вершин ведет специальная входная стрелка.
Помеченные стрелки называются плюс - стрелками, а непомеченные- минус - стрелками.
В графе есть только одна вершина, не имеющая выходной стрелки, называемая конечным оператором.
Каждому распознавателю сопоставляется логическое условие
F - произвольная функция алгебры логики, зависящая от k логических переменных p1,p2,…,pk.
Каждому оператору А, кроме конечного, приписывается некоторый набор P (p1,p2,…pk) логических переменных, называемых сдвигом по логическим переменным.
Оператор А с приписываемым ему сдвигом обозначается А(P).
Совокупность сдвигов P1,P2,…,Pn всех операторов А1,A2,…,An операторной схемы Янова называется распределением сдвигов, приписываемых схеме G.
Если для любого i (1<=i<=n) Pi=∩ (пустое множество), то распределение сдвигов называется пустым, при Pi=(p1,p2,…,pk) распределение сдвигов называется универсальным.
Все операторы одной операторной схемы считаются попарно различными.
Операторная схема Янова G с операторами A1,…,An и логическими переменными p1,…,pk обозначается G(A1,…,An,p1,…,pk).
Пример операторной схемы Янова может выглядеть следующим образом:
Для операторной схемы G определим понятие конфигурации, строящейся с помощью порождающего процесса блуждания по схеме G, задаваемого по индукции. Конфигурация получается в виде двойной последовательности наборов значений логических переменных p1,p2,…,pn и символов операторов А1,A2,…,An, записываемых в виде двух строк: верхней для наборов и нижней для операторов.
Построение конфигурации осуществляется следующим образом.
В верхнюю строку записывается произвольный набор D. нижняя строка пуста.
Движение по схеме G начинается в направлении, указанном входной стрелкой. Если стрелка приходит к распознавателю R(F), то вычисляется F(D).
Если F(D)=1, то с тем же набором движение продолжается по плюс -стрелке, выходящей из распознавателя R., в противном случае, движение происходит по минус -стрелке.
Если стрелка приводит к оператору A(P), то символ оператора А выписывается в нижнюю строку конфигурации и набор D преобразуется в набор D1, который в свою очередь выписывается в верхнюю строку. Дальнейшее движение продолжается по стрелке, выходящей из А.
Если стрелка приводит к конечному оператору, то его символ выписывается в нижнюю строку и построение конфигурации завершается.
При движении по распознавателям возможен случай, когда, не попав ни на один из операторов, мы снова придем к недавно пройденному распознавателю. В этом случае движение по распознавателю станет бесконечным. При обнаружении такого цикла движение искусственно прерывается и в нижнюю строку ставится символ пустого периода ( ).
Верхняя последовательность наборов называется допустимой последовательностью s наборов для схемы G , нижняя последовательность операторов называется значением z схемы G , определяемым допустимой последовательностью s.
Поскольку при построении конфигурации возможен произвол в выборе начального набора значений логических переменных, то каждой схеме G можно сопоставить некоторое множество конфигураций K(G), являющееся в общем случае бесконечным.
Рассмотрим две конфигурации для предложенного примера.
При D=10
10
A1( ) X
При D=11
11 00 11
A1(p,q) A1(p,q) ( )
Отношение эквивалентности определяется для любой пары операторных схем G1 и G2 с одними и теми же логическими переменными p1,p2,…,pk.
Схемы G1 и G2 являются эквивалентными, если K(G1)=K(G2),то есть, если совпадают их множества конфигураций.
Система правил преобразования операторных схем Янова построена в виде логического исчисления, т.е. совокупности аксиом и правил вывода.
Аксиомы постулируют безусловную возможность замены некоторого фрагмента операторной схемы на другой фрагмент, предписываемый данной аксиомой.
Правила вывода постулируют возможность замены одного фрагмента на другой при выполнении некоторых условий, содержащихся в посылке данного правила вывода.
Фрагментом операторной схемы G называется некоторая часть схемы G , для которой указана связь с остальными вершинами схемы G. Эта связь указывается в виде входов и выходов фрагмента.
Входы фрагмента – это различные стрелки, показывающие, к каким вершинам фрагмента ведут стрелки от остальных вершин схемы. Входы фрагмента могут быть указаны в виде обобщенного входа, который указывает, к какой вершине может вести произвольная совокупность стрелок, выходящих либо от остальных вершин схемы, либо от выходов этого же фрагмента.
Выходы фрагмента – это различные стрелки, которые показывают, какие вершины фрагмента соединены с остальными вершинами схемы. Входы метятся римскими цифрами, выходы - арабскими.
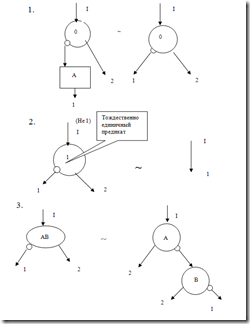
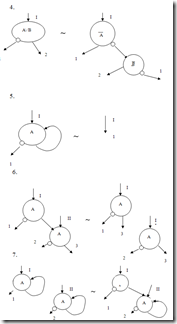
Аксиомы и правила вывода представлены ниже:
Применяя аксиомы 1-7 можно получить логическую схему алгоритма гарантированно эквивалентную исходной.
Правила вывода для логических схем алгоритмов имеют вид:
Примечание
Некоторый распознаватель R(A) подчинен логической функции В, если проверка R(A) при выполнении схемы производится только для тех значений логических переменных, для которых В истинно.
В правилах вывода над чертой записывается посылка, а под чертой – утверждение.
Буквой F обозначаются фрагменты, Λ- пустые фрагменты.
Для любых логических схем справедлива теорема Янова, которая утверждает следующее:
Любые две равносильные операторные схемы эквивалентны.


0 коммент.:
Отправить комментарий