Во всех рассмотренных нами циклических кодах длина кодовых слов однозначно определяется степенью выбранного примитивного многочлена. Это обстоятельство накладывает большие ограничения на число информационных разрядов в кодируемом блоке. Между тем, в используемых в настоящее время стандартах передачи данных, длина информационных блоков может колебаться в довольно широких пределах. В соответствии с этим, кодирование также должно быть достаточно гибким.
Здесь на помощь приходят укороченные коды, построенные на основе циклических кодов. Пусть, например, нами выбран многочлен с т = 5. На базе этого многочлена можно построить циклический (31,26)-код Хэмминга. Рассмотрим подможество слов этого кода, содержащее все кодовые слова с тремя нулями в старших разрядах1 Это подмножество образует укороченный (28,23)-код Хэмминга. Укороченный код сохраняет все свойства циклического (31,26)- кода, так как в процессе декодирования мы можем дописать к кодовым словам три недостающих нуля и рассматривать их как векторы основного (31,26')-кода Хэмминга.
В качестве следующего примера можно привести код Файера, используемый в мобильной связи. Этот код является сильным укорочением кода Хэмминга. Соответствующий код Хэмминга имеет непомерно большую дайну, равную 3014633 и содержит 40 проверочных символов. На его базе строится (224,184)-код Файера, способный обнаруживать все пакеты ошибок длиной до 40 символов, или исправлять все пакеты длиной до 12 символов. Этот код может эффективно бороться с замираниями и используется в мобильной связи GSM для защиты канала управляющей информации SACCH (Slow Associated Control Channel).
Таблица 3.9. (6,3)-код.
| Вход | Кодовое слово |
| ООО | 000 000 |
| 100 | 110 100 |
| 010 | 011 010 |
| 110 | 101 110 |
| 001 | 111 001 |
| 101 | 001 101 |
| 011 | 100 011 |
| 111 | 010 111 |
Из примера кода Файера видно, что использование при кодировании простого дополнения информационного слова нулями практически неприемлемо, поэтому должен применяться более эффективный метод кодирования укороченных кодов.
Пример: Укороченный (6,3)-код.
Рассмотрим метод кодирования и декодирования кода, полученного укорочением (7,4)-кода Хэмминга. Выберем из множества кодовых слов базового кода все кодовые слова, начинающиеся с символа «О». Выбрасываемые при укорочении символы полагаются равными нулю и, поэтому, не передаются. Таким образом получаем укороченный (6,3)~код. В левой части таблицы 3.3 приведены кодовые слова (7,4)-кода Хэмминга, у которых старший разряд равен нулю. Выбрасывая из этих слов лишние нули, получаем кодовые слова укороченного (6,3)-кода (см. табл. 3.9).
Замечание. Построенный (6,3)-код не является циклическим, так как циклический сдвиг кодовых слов не во всех случаях является кодовым словом, однако, его конструкция позволяет использовать свойства циклических кодов при декодировании.
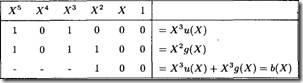
Проверим таблицу 3.9 с помощью алгоритма деления Евклида. Рассмотрим информационный вектор и = (101), многочлен которого и(Х) = 1 + X2. Умножая и(Х) на X3 и используя алгоритм деления Евклида (см. табл. 3..10), получим многочлен остатка от деления Х3и(Х) на g(X) = 1 + X + X3, равный b(X) = X2. Таким образом,
Таблица 3.10. Определение проверочных символов (алгоритм деления Евклида) для и(Х) 1 1 А1 и д(Х) = 1 +Х + Х3.
многочлен систематического (6,3)-кода равен v{X) = Х3и{Х) + Ь(Х) = Х3[Х[1] + 1] + X2 = Хъ + X3 + X2, (3.91)
что соответствует кодовому вектору v = (001 101) из табл. 3.9.
За основу кодера систематического (6,3)-кода может быть принята схема кодирования, приведенная на рис. 3.8. Так как (6,3)-код образуется укорочением (7,4)-кода Хэмминга, схема рис. 3.8 существенно упрощается: из регистров удаляются разряды из и vg и кодирование заканчивается уже после третьего такта.
Для практической реализации декодера укороченного кода имеются три альтернативы:
1. Для декодирования (6,3)-кода можно, в принциие, использовать декодер базового (7,4)-кода Хэмминга (см. рис. 3.20). В этом случае, к принятому слову приписывается недостающий ноль и процесс декодирования занимает столько же тактов, сколько требуется для декодера базового кода.
Для декодирования кодов с 2-кратным укорочением необходимо затратить I дополнительных тактов. В случае, когда I велико (как, например, в случае кода Файера) такой метод декодирования неприемлем.
«не знает об укорочении») и следующим за синдромом «111» будет синдром «101». В соответствии с его числовым вектором и производится модификация текущего синдрома на рис. 3.22.
Замечание. В силу линейности кодов и схем их реализации, рассмотренный метод декодирования может быть применен для любых укорочений кода Хэмминга.
Такой метод декодирования, в ряде случаев, приводит к достаточно простой схеме построения декодеров и, поэтому, весьма интересен для практики. В качестве примера в [4] приведена схема декодирования укороченного (272,260)-кода.
3. Этот вариант построения декодера Меггита особенно интересен для практики, так как используемые в нем алгоритмы распознавания ошибок и коррекции синдрома не зависят от длины укорочения I и строятся с наименьшими затратами. Длина укорочения учитывается путем умножения принятого слова на некоторый многочлен, зависящий от I.
На примере укороченного (6,3)-кода мы покажем, как могла бы выглядеть оптимальная процедура распознавания ошибки в компоненте Г5 и коррекции соответствующего синдрома. Как уже отмечалось ранее, в нижнем регистре рис. 3.22 производится вычисление синдромов циклических сдвигов вектора ошибки для неукороченного (7,4)-кода Хэмминга, поэтому таблицу 3.6 можно использовать и для (6,3)-кода с учетом того, что первым вычисляется синдром для es = (ООО 0010). На последующих тактах в нижнем регистре вычисляются синдромы для
и т. д. Наиболее благоприятным с точки зрения затрат на модификацию в схеме рис. 3. 22 является синдром s = (0,0,1). Из таблицы 3.6 следует, что этот синдром соответствует вектору ошибки
т.е. ошибке в компоненте Г2- Таким образом, для реализации оптимальной процедуры исправления ошибки и коррекции синдрома в схеме рис. 3.22 необходимо предварительно произвести четыре циклических сдвига верхнего и нижнего регистров (при этом верхний регистр должен быть модифицирован: в него должны быть добавлен дополнительный разряд Гб и цепь обратной связи (Прим. переводчика)).
На примере укороченного (6,3)-кода может показаться, что эти затраты не слишком велики, однако, для используемого в сети GSM кода Файера миллион и более сдвигов плюс затраты на модификацию регистра оказываются технически неприемлемыми. Ниже мы теоретически покажем, что дополнительные затраты такого рода отнюдь не. являются необходимыми. После этого мы рассмотрим построение схемы оптимального декодера укороченного (6,3)-кода.
Будем искать схему построения декодера укороченного кода, в которой технические затраты на исправление ошибки и коррекцию синдрома были бы минимальными. Так как базовый (п, к)-код является циклическим, эта схема должна обнаруживать и исправлять ошибку в младшем разряде кодового слова укороченного (п—1,к — 1)- кода. Многочлен такой ошибки имеет вид
где I - длина укорочения.
Постараемся найти линейную операцию, отображающую е(Х) в некоторый вспомогательный многочлен е'(Х), синдром которого при е(Х) = Хп~1~1 был бы равен
Пусть такая операция отображает многочлен е(Х) = Хп 1 1 в
Так как степень многочлена е'(Х) меньше степени д{Х), равенство (3.93) остается справедливым. Заметим, что е'(Х) = Хп~к~1 можно получить из многочлена е(Х) = Х"'1-1, г-кратным циклическим сдвигом, то есть
При этом после 1 + 1 первых сдвигов е'(Х) = Х°, а после оставшихся п — к — 1 сдвигов выполняются равенства (3.94) и (3.93). Постараемся заменить операцию г-кратного циклического сдвига линейной операцией умножения многочленов.
Из соотношения (3.9) следует, что в нашем случае справедливо равенство
где д(Х) - некоторый многочлен, конкретное значение которого не представляет для нас интереса. Согласно теореме 3.2.5, порождающий многочлен д(Х) делит Хп + 1 без остатка, поэтому можно записать
Применяя алгоритм деления Евклида, сомножитель Хг можно представить в виде
Подставляя (3.98) и (3.99) в (3.97), имеем
Из (3.100) следует
квадратных скобках умножено на д(Х) и, следовательно, это произведение не оказывает влияние на синдром в правой части (3.101). Таким образом, мы имеем
Обобщая все вышесказанное, можно сделать следующие выводы:
2. Ошибка обнаруживается при ее сдвиге в старший разряд кодового слова укороченного (п — 1,к — /)-кода и исправляется на следующем такте работы декодера;
3. В схеме декодера вычисляется синдром вспомогательного многочлена е'(Х) = e(X)d(X). В этом случае ошибке е(Х) = Хп~1~1 соответствует синдром s'(X) = Хп~к~г, который также корректируется на следующем такте;
4. Многочлен d(X) является остатком от деления Хг на д(Х), где г определяется длиной укорочения I и степенью производящего многочлена д(Х);
5. Так как степень многочлена d(X) всегда меньше степени д(Х), схема умножения е(Х) на d(X) может быть реализовала с помощью простых сдвигов.
Пример: Укороченный (6,3)-код.
и вспомогательный многочлен е'(Х) равен
Рассмотрим построение оптимального, с точки зрения затрат, декодера'укороченного (6,3)-код. Напомним, что этот код образуется укорочением базового циклического (7,4)-кода Хэмминга с порождающим многочленом д(Х) = 1 + X + X3. В этом случае многочлену ошибки е(Х) = X5 должен соответствовать синдром вспомогательного многочлена s'(X) = X2. Так как X2 является четырехкратным циклическим сдвигом многочлена е(Х) = X5, множитель d(X) определяется как
Таким образом, в схеме рис. 3.23 вектор ошибки через сумматоры однавременно подается на разряды si и S2 регистра вычисления синдрома. На рис. 3.23 приведен пример вычисления синдрома для е = (0,0,0,0,0,1), то есть синдрома ошибки, находящейся в старшем разряде укороченного (6,3)-кода. Как и следовало ожидать, после шестого такта мы получаем синдром s' = (0,0,1).
Схема исправления однократной ошибки и коррекции синдрома с использованием вспомогательного многочлена е'(Х) приведена на рис. 3.24. По вычисленному синдрому s' = (0,0,1) происходит обнаружение и исправление ошибки. Одновременно синдром корректируется и, тем самым, устраняется влияние ошибки на последующие шаги декодирования.
Таблица 3.11. Вычисление синдрома неискаженного принятого слова п = (0,1,1,0,1,0).
Таблица 3.12. Вычисление синдрома неискаженного принятого слова ri = (0,1,1,0,1,1).
Проверим работу декодера на трех примерах. Пусть кодовое слово Г} = (0,1,1,0,1,0) (см. табл. 3.9) принято без ошибок. Последовательность состояний регистра синдрома приведена в табл. 3.11. После окончания загрузки слова ri в буфферный регистр, в нижнем регистре также заканчивается вычисление его синдрома. В данном случае синдром оказывается нулевым.
Теперь в старший разряд слова ri внесем одну ошибку и получим вектор гг = (0,1,1,0,1,1). После загрузки слова гг в буфферный регистр, его синдром равен s'2 = (0,0,1) (см. табл. 3.12). Согласно алгоритму декодирования, такой синдром указывает на ошибку в старшем разряде слова Г2-
Таблица 3.13. Вычисление синдрома искаженного принятого слова гз = (0,1,0,0,1,0).
И, наконец, рассмотрим декодирование принятого слова с ошибкой в третьей компоненте: гз = (0,1,0,0,1,0). Синдром принятого слова гз равен s^ = (1,0,1) (см. табл. 3.13). Это означает, что в принятом слове имеется ошибка, но она произошла не в старшем разряде, поэтому продолжим процедуру вычисления синдромов теперь уже для сдвигов слова Гз (см. табл. 3.14).
Эта процедура продолжается до тех пор, пока ошибочная компонента гз не займет место старшего разряда. После этого синдром принимает значение S3 = (0,0,1) и происходит исправление ошибки и коррекция синдрома. Далее декодирование происходит уже с нулевым синдромом, то есть после исправления ошибки в третьей компоненте мы получили слово (6,3)-кода.







0 коммент.:
Отправить комментарий