Телеграфный код №2 (код Бодо) трудно защитить от помех так как он не имеет избыточности. Чтобы уменьшить число ошибок следует выделить группу символов нуждающихся в усиленной защите, и подбирать комбинации кода таким образом чтобы уменьшить вероятность перехода передаваемых символов в запрещенный символ. С использованием избыточности цифровые данные передаваемые двоичными кодами, можно защитить от искажений, например, выделив группу кодов с постоянным количеством нулей и единиц, либо просто с четным числом единиц или нулей тогда при искажении одного из символов ошибка будет обнаружена. В пятизначном двоичном коде с постоянным соотношением нулей и единиц может быть:
Если выбрать для передачи цифр комбинации или
процент необнаруженных ошибок резко уменьшится.
Стандартный код №3 относится к кодам с постоянным весом и сам по себе обладает корректирующими способностями, так как все его комбинации из трех единиц и четырех нулей (см. приложение 4). Нарушение этого соотношения свидетельствует об ошибки стандартный телеграфный код номер 3, или, как его еще называют, 3:4 (три к четырем), обнаруживает все одиночные ошибки и все ошибки нечетной кратности.
Инверсные коды обычно образуются добавлением к информационной комбинации и ее инверсии. Например, инверсные коды мы сможем получить, если к рассмотренным выше комбинациям кода добавим в том же порядке комбинаций
, являющиеся их инверсиями
и т. д.
Процесс исправления одиночной ошибки на приемном конце может осуществляется суммированием по модулю 2 информационной и проверочной частей кода. Если ошибки в принятом коде нет, опознаватель будет состоять из одних единиц:
| 1 1 0 0 0 | |
| 0 0 1 1 1 | |
| 1 1 1 1 1 | |
Предположим при передаче кода 1100000111 ошибки произошли при первой передаче в первом разряде, а при второй – в третьем разряде в этих случаях опознаватели будут иметь вид:
| 0 1 0 0 0 | 1 1 1 0 0 | ||
| 0 0 1 1 1 | 0 0 1 1 1 | ||
| 0 1 1 1 1 | 1 1 0 1 1 | ||
Рис. 5
Как видим, место нуля в опознавателе указывает место ошибки в информационной части кода. Если в опознавателе число нулей больше двух – комбинация бракуется.
Обнаружение ошибок на физических носителях информации обычно сводится к различным проверкам на четность.
Если на четность символы проверяются в порядке их нанесения наносите (например, перфоленту, то такая проверка называются вертикальной (рис. 5, а).
Если на четность символы проверяются по строкам, то такая проверка называется горизонтальной (рис. 5, б). При этом способе проверки устанавливается строго фиксированная длина строки, которая определяется либо в зависимости от объема данных, которые переносятся на перфоленту либо длиной ленты рулонного аппарата, либо в зависимости от частоты контроля принимаемой информации.Каждая из этих проверок позволяет обнаружить все одиночные и все ошибки нечетной кратности. Ошибки четной кратности не обнаруживаются.
Если с каждым шагом по строке линия проверки смещается на один шаг по столбцу, то такая проверка называется спиральной(рис. 5, в).
Спиральная проверка позволяет обнаруживать большой процент ошибок четной кратности, так как в этом случае смежные ошибочные разряды попадают в различные линии проверки.
Если на четность символы проверяются и по строкам, и по столбцам, то такая проверка называется перекрестной (рис. 5, г). При перекрестной проверке минимальное кодовое расстояние 4.
Часто корректирующие способности закладываются непосредственно в коды, из которых составляются сообщения. Например алфавитно-цифровые коды, СПМ, в своем большинстве содержат два отверстия на букву, алфавитно-цифровой код «3 из 6» содержит по 3 пробивки в каждой половине перфокарты и т. д.
Контроль по модулю заключается в том, что для обнаружения ошибок используется признак делимости, а в качестве проверочных разрядов к кодовой комбинации дописывается разрешенный остаток от деления.
В качестве делителя следует использовать простые числа 2, 3, 5, 7, 11, 13, … . Запись соответствия числа заданному условию по признаку делимости имеет вид
Читается эта запись так: число А сравнимо с числом К по модулю М[1], т. е. при делении числа А на М в остатке окажется число К. Например, 490 (модуль 7); 50
1 (модуль 7); 25
4 (модуль 7). Передаваемые цифровые коды будут иметь вид соответственно: 490; 501; 254.
Контроль по сумме и контроль по произведению могут рассматриваться как модификация метода контроля по модулю. Машина производит автоматическое суммирование цифр, затем производится деление на модуль. Если ошибок нет в остатке должен быть 0. Для того чтобы упростить процесс нахождения проверочного разряда, его выбирают таким чтобы цифры информационных и проверочного разрядов давали в сумме число, равное выбранному модулю (см. задачу 7.17).
Контроль по произведению является более надежным методом с точки зрения обнаружения ошибок. При контроле по произведению проверочный разряд находится как дополнение к сумме произведения цифр информационных разрядов на номер информационного разряда. Результат сложения суммы произведений с проверочныразрядом должен давать число, которое делиться на выбранный модуль без остатка (см. задачу 7.20).
Обнаружение ошибки (с указанием места ошибки) на основе использования принципа делимости может быть осуществлено для кодов с соотношением информационных и проверочных разрядов, соответствующих табл. 1 приложения 8.
Схема вычисления проверочных знаков для кода с четырьмя информационными и тремя проверочными знаками приведена в табл. 7.1.
Таблица 7.1 | ||||||
| Информационные разряды | Проверочные разряды | |||||
| тысяч | сотен | десятков | единиц | А | В | С |
| - | А | А | А | А | - | - |
В | - | В | В | - | В | - |
С | С | - | С | - | - | С |
Нахождение значения проверочного разряда производится следующим образом. Проверочный знак А образуются дополнением до числа, кратного выбранному модулю, суммы цифр, стоящих в разряде сотен, десятков и единиц; В – тысяч, десятков и единиц; С– тысяч, сотен и единиц.
Адрес ошибки обнаруживается по следующему правилу если проверочные разряды полученного числа отличаются во всех трех знаках А, В, С (см. табл. 7.1), то ошибка в разряде единиц. А если отличие в знаках А и В – ошибка в разряде десятков, в А и С – в разряде сотен, В и С – в разряде тысяч. Если расхождение в одном разряде, то ошибка в самом проверочном разряде.
В случае обнаружения ошибки правильная цифра находится по следующей формуле:
где - ошибочная цифра; К – правильная цифра проверочного разряда1;
- цифра проверочного разряда, полученная в результате контрольных проверок.
Если величина Z получится отрицательным числом, то следует брать ее дополнение до модуля. Если величина Z получается больше модуля, то от Z вычитается значение модуля (числовой пример см. задачи 7.23, 7.25 и 7.27).
Обнаружение ошибок по запрещенной части запрещенной комбинации, основано на том, что из общего числа кодов данной длины выбирают часть кода с кодовым расстоянием d2, остальные кодовые комбинации считаются запрещенными, появление запрещенной комбинации говорит о наличии ошибки. Например, если пятизначный двоичный код разделить на две части таким образом, чтобы в одной части были комбинации только с четным количеством единиц, а во второй - нечетным, то получаются два отдельных кода, обнаруживающих, одиночную ошибку, либо в случае кодов с постоянным весом разрешенными считаются только комбинации,имеющие одинаковое количество единиц и т. д.
В случае распространенные в практике механизированной обработки цифровых кодов в памяти машины записывается кодовая книга – перечень разрешенных комбинаций. Каждая вновь поступившая комбинация сравнивается с разрешенными по кодовой книге и, если среди разрешенных комбинаций нет поступившей вырабатывается сигнал ошибки. В приложении 11 приведены кодовые книги с минимальным кодовым расстоянием соответственно и
.
Первая позволяет обнаруживать ошибки, вторая обнаруживать и исправлять. Процесс исправления одиночной ошибки происходить путем отыскивания в кодовой книге числа, совпадающего в любых трех из четырех разрядов. Если число совпадает по трем разрядам, то исправляют ошибку, заменяя ошибочную цифру на ту что находится в четвертом разряде числа кодовой книги (см. задачу 7.33).
Комбинированный инверсный код обладает способностью исправлять одиночную и обнаруживать двойные ошибки в пятизначных двоичных комбинациях. Достоинства кода – простота аппаратуры реализующей алгоритм декодирования.
Избыточность такого кода 50%. Число информационных разрядов равно числу корректирующих.
Код строится по следующему правилу: если в информационной части кода число единиц нечетно, то корректирующая часть кода состоит из таких же символов, что и информационная часть: если число единиц в информационной части кода четно, то корректирующая часть кода представляет собой инверсию информационной части.
По виду вектора, полученного в результате суммирования по модулю два первой и второй частей принятой кодовой комбинации, можно судить о том четно или нечетно число единиц в информационной части кода. Это обстоятельство придает дополнительные корректирующие возможности коду. Если вектор суммы содержит преобладающее число единиц, то сумма единиц в информационной части кода должна быть четна, а место нуля в векторе суммы
указывает место ошибки (в случае одиночной ошибки). Если вектор суммы содержит преобладающее число нулей, то число единиц в информационной части кода должно быть нечетно. Место ошибки указывает разряд, содержащий единицу в векторе суммы.
1 Если ошибка в разрядах А, В, С, то контрольные разряды правильные; если ошибка в контрольном разряде, то правильное значение ошибочного разряда находится суммированием разрядов А, В, С, в которых в этом случае ошибки нет. Двойные ошибки этим методом не обнаруживаются.

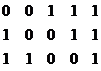

0 коммент.:
Отправить комментарий