Бинарные деревья

В математике бинарным (двоичным) деревом называют конечное множе­ство вершин, которое либо пусто, либо состоит из корня и не более чем двух непересекающихся бинарных деревьев, называемых левым и правым подде­ревьями данного корня.

Таким образом, каждая вершина бинарного дерева может включать одно или два поддерева или не включать поддеревьев вовсе. Первое поддерево обычно называют левым, а второе - правым. Соответственно ветвь, исходя­щую из вершины и ведущую в корень левого поддерева, называют левощ а ветвь, ведущую в корень правого поддерева - правой. Вершины, из которых не выходит ни одной ветви, называют листьями (рис. 7.17).

В программах для реализации бинарных деревьев используют п-связные списки. С вершинами бинарного дерева обычно связывают записи, хранящие некоторую информацию.

Построение дерева выполняется следующим образом. Если дерево пус­то, то первая же вершина становится корнем дерева. Добавление остальных вершин регламентируется в зависимости от условия задачи: в соответствии с заданной дисциплиной построения дерева отыскивается подходящая верши­на, к которой й подсоединяется новая вершина.

Достаточно часто используют регулярные бинарные деревья с разными законами построения. Примером могут служить сортированные бинарные деревья, построение которых осуществляется по правилу: ключевое поле ле­вого поддерева всегда должно содержать значение меньше, чем в корне, а ключевое поле правого поддерева - значение больше или равное значению в корне.

Рассмотрим основные операции с сортированными бинарными деревь­ями.

Исходные установки. В начале программы необходимо описать эле­мент и его тип:

Type topjptr=*top; {тип «указатель на вершину»} top=record

value:integer; {число}

left, {указатель на левое поддерево}

right:topj)tr; {указатель на правое поддерево} end;

В статической памяти описываем указатель корня дерева и несколько указателей, используемых при выполнении операций со списком:

Var root, {указатель структуры - адрес корня дерева} pass, next, q:topjptr; {вспомогательные указатели}

Исходное состояние - «пустое дерево»: root:-nil;

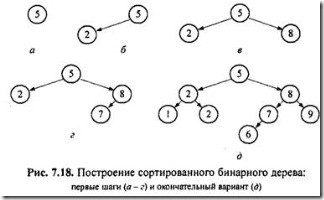
Построение дерева. Дерево строится в соответствии с главным прави­лом. Например, пусть дана последовательность целых чисел {5, 2, 8, 7, 2, 9, 1, 5}. Первое число 5 будет записано в корень дерева (рис. 7.18, а). Второе число 2 меньше значения в корне дерева, следовательно, оно будет записано в левое поддерево (рис. 7.18, б). Следующее число 8 больше значения в кор­не, соответственно оно будет записано в правое поддерево (рис. 7.18, в). Сле­дующее число 7 больше, чем значение в корне дерева, значит, оно должно быть записано в правое поддерево, но правое поддерево уже построено. Сравниваем 7 со значением в корне правого поддерева - числом 8. Так как добавляемое значение меньше значения в корне правого поддерева, то добав-

ляем левое поддерево уже к этому корню (рис. 7.18, г). Полностью сформи­рованное бинарное дерево представлено на рис. 7.18, д.

Фрагмент программы, реализующий добавление вершины к дереву, со­стоит из трех частей: создания вершины, поиска корня, к которому можно до­бавить поддерево, придерживаясь основного правила, и, непосредственно, добавления вершины:

{создание новой вершины}

new(q); {выделяем память для нового элемента} with q^A do {заносим значения} begin value—п; left—nil; right.—nil;

end;

{поиск корня для добавляемой вершины}

pass:=root; {начинаем с корня бинарного дерева}

whilepass<>nil do {пока не найдено свободное место} begin next—pass; {сохраняем адрес корня-кандидата}

if q ^А. value <pass^A value then pass—pass ^A. left {влево}

else pass—pass^A right; {вправо}

end;

{добавление вершины}

if q^Avalue<next^A value then {если значение меньше корня} next^A.left:=q {добавляем левое поддерево} else next^A right—q; {добавляем правое поддерево}

Используя рекурсивцость определения дерева, можно построить рекур­сивную процедуру добавления вершин к дереву. В качестве параметров эта процедура будет получать указатель на корень дерева и указатель на добав­ляемый элемент.

Procedure Add(Vdr r:topjptr; pass:topjptr); begin

if r=nil then r.—pass {если место свободно, то добавляем} else {иначе идем налево или направо}

if (pass^A.value<r^A.value) then Add(r^A.left_ypass)

else Add(r^. right, pass);

end;...

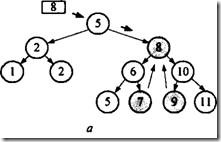
Поиск вершины в сортированном бинарном дереве. Поиск в сорти­рованном бинарном дереве осуществляется следующим образом: вначале значение ключа поиска сравнивается со значением в корне. Если значение ключа в искомой вершине меньше, чем в корневой, то поиск переходит в ле­вую ветвь. Если больше или равно - то в правую ветвь. И так в каждой сле­дующей вершине до тех пор, пока не отыщется искомая. Так, для предыду- щего варианта последовательности поиск вершины с ключом 7 будет выполнен за три шага (рис. 7.19).

Если мы добрались до листа, а иско­мая вершина не обнаружена, то следует выдать соответствующее сообщение. В противном случае вершину помечают как найденную (запоминают ее адрес) и обра­батывают в соответствии с алгоритмом программы:

pass:=root; {начинаем с корня бинарного дерева}

flag:=false; {признак «вершина не найдена»}

while (pass<>nil) and not flag do {пока не найден элемент или не до­шли до листа} if n=pass^A.value then flag:-true {значение найдено} else

if n<pass\value then pass:-pass^Aleft {влево}

else pass:-pass^A right; {вправо}

if flag then < вершина найдена>

else <вершина не найдена> ...

Поиск вершины также можно осуществлять, используя рекурсию. Для удобства использования построим рекурсивную функцию, которая будет возвращать true, если элемент найден, и false - в противном случае. Адрес найденного элемента будем возвращать через параметр pass:

Function Find(r:topjptr; Var pass:topjptr; n:integer):boolean;

Begin

ifr=nil then Find:=false {значение не найдено} else

ifn=r^A.value then begin

Find:-true; {значение найдено} pass:=r; {запомнили адрес} end

else

if n<r^A.value then

Find: =Find(r*. left, n) {влево} else Find: =Find(r*.right_fn); {вправо}

End;

Вызывать такую функцию можно непосредственно из условия операто­ра условной передачи управления или циклов, например:

if Find(r,pass,n) then <вершина найдена, адрес в pass> else < вершина не найдена> ...

Удаление вершины с указанным ключом. Удалению вершины с ука­занным ключом предшествует ее поиск (см. выше). Непосредственное удале­ние вершины реализуется в зависимости от того, какая вершина удаляется:

• удаляемая вершина не содержит поддеревьев (лист) - удаляем ссыл­ку на вершину из корня соответствующего поддерева (рис. 7.20);

• удаляемая вершина содержит одну ветвь (рис. 7.21, а): для удаления необходимо скорректировать соответствующую ссылку в корне, заменив ад­рес удаляемой вершины адресом вершины, из нее выходящей (рис. 7.21, б);

• удаляемая вершина содержит две ветви (рис. 7.22, а): в этом случае нужно найти подходящую вершину, которую можно вставить на место уда­ляемой, причем эта подходящая вершина должна легко перемещаться. Такая вершина всегда существует: это либо самый правый элемент левого подде­рева, либо самый левый элемент правого поддерева удаляемой вершины (рис. 7.22, б).

Ниже представлена рекурсивная процедура удаления вершины с указан­ным значением (параметры: г - адрес корня дерева, к - значение).

Procedure Delete(var r:top j)tr;k:integer);

{Внутренняя рекурсивная процедура поиска заменяющей вершины в левом поддереве. Параметры: г - адрес корня левого поддерева, q - адрес заменяемой вершины} Procedure del(var r:top_ptr; q:top_ptr); Var ql:topjptr; begin

if r\right=nil then {заменяющая вершина найдена} begin

q^A.value:-r\value; {копируем значение} ql:=r;

r:-r\left; {удаляем заменяющую вершину}

Dispose(ql); {освобождаем память} end

else del(r\right,q) {идем по поддереву направо} End; Var q:top_ptr; begin

if r=nil then WriteLnC3nmeHm не найден или дерево пустое *) else {поиск элемента с заданным ключом}

if k<r^A.value then {если меньше, то налево} Delete(r^Aleft,k)

else

if k>r^A value then {если больше, то направо} Delete (г*, right, к)

else

begin {элемент найден, его необходимо удалить} {удаление листа или корня с одним поддеревом} if r^Aright=nil then {нет правого поддерева} begin q:=r; r:=r^A.left; Dispose(q); end

else

if r^AJeft=nil then {нет левого поддерева} begin

r:-r^A, right; Dispose(q);

end

else {удаление корня с двуми поддеревьями}

del(r^Aleft,r);

end End;...

Сортировка с использованием дерева. Так как дерево формируется по определенным выше правилам, то сортировка по возрастанию осуществля­ется обходом дерева «слева направо». Обход начинается с самого нижнего левого листа или, если такого листа нет, корня. Вывод значений осуществля­ется в следующем порядке: сначала выводится значение самого нижнего ле­вого поддерева, затем корня, затем самого нижнего левого поддерева право­го поддерева и т.д. (рис. 7.23).

Пример 7.6. Разработать про­грамму сортировки заданной по­следовательности целых чисел с использованием сортированного бинарного дерева.

Программа должна строить бинарное дерево из вводимых с клавиатуры целых чисел, а затем осуществлять обход дерева для вывода отсортированных данных.

Построение дерева реализуем отдельной подпрограммой, которая будет получать адрес добавляемой вершины и адрес корня бинарного дерева. По­иск корня для добавляемой вершины, как показано выше, будем осуществ­лять рекурсивно.

Обход дерева «слева направо» также будем осуществлять рекурсивно. Нерекурсивный вариант достаточно сложен, и его использование нецелесо­образно.

Полностью текст программы приведен ниже. Program Sort4;

Type topjptr=^Atop; {тип "указатель на вершину дерева"} top=record {тип вершины дерева}

value:integer; {целое число}

left, right:topjptr; {указатели на левое и правое поддеревья} end;

Var next number:integer;

r, pass:topjptr; {корень бинарного дерева} {процедура добавления вершины к дереву}

Procedure Add (Var r:topjptr; pass:topjptr); begin

if r=nil then repass {если место свободно, то добавляем} else {иначе идем налево или направо}

if (pass^Avalue<r^A value) then Add(r^A.left,pass)

else Add(r^A. right,pass);

end;

{процедура сортировки - обход дерева}

procedure Tree(r:topjptr); begin

if r<>nil then

begin {если есть поддерево}

Tree(r^A.left); {обход левого поддерева} Write(r^A value:4); {вывод значения из корня} Tree(r^A right); {обход правого поддерева} end;

end;

{основная программа}

begin

{формирование исходного дерева} WriteLnCBeodume числа); г:-nil;

Read(nextjiumber); while not EOF do

begin

new(pass); {выделяем память для нового элемента} withpass^A do {заносим значения} begin

value: =nextjiumber; left: -nil; right: -nil; end;

Add(r, pass); {добавляем элемент к дереву} Read(nextjiumber)

end;

ReadLn;

WriteLnCCopmupoeaHuan последовательность: ');

Tree(r);

End

Оценка вычислительной сложности операций с сортированными бинарными деревьями. Использование сортированных бинарных деревьев достаточно эффективно с точки зрения временных оценок. Оценим вычисли­тельную сложность основных операций с данной структурой.

Операция поиска вершины. Худшим случаем при поиске вершины явля­ется случай, когда дерево имеет вид последовательности вершин (рис. 7.24, а, б). В этом случае для поиска вершины в среднем потребуется (п+1)/2 проверок, как при последовательном поиске, например, в массиве, или О_х(п).

Оценку в среднем выполним для сбалансированного дерева (рис. 7.24, в). Поиск вершины в этом случае потребует (log₂ п+1)/2 проверок, т. е. получаем вычислительную сложность в среднем O_cp(log₂ п).

Операция построения дерева. Худшим случаем при построении дерева является дерево, представляющее собой последовательность вершин, так как при этом поиск вершины, к которой необходимо добавить новую, потребует максимального числа проверок. Количество проверок в этом случае: п-1 - для последнего элемента, 1 - для второго (для первого элемента проверки не

требуется). В среднем необходимо [(п-1)+1]/2 проверок; умножив на п-1 элемент, получаем п(п-1)/2 проверок, или О_х(п²).

Оценку в среднем выполним также на сбалансированном дереве. Коли­чество проверок для поиска родительской вершины составит (log₂ (п-1 )+1 )/2; соответственно, умножив на (п-1), получим O_cp(nlog₂ п).

Операция обхода дерева в процессе получения сортированной последо­вательности. Для деревьев обоих видов сложность одинакова, так как для каждой вершины при обходе проверяется наличие левого и правого поддере­вьев, т.е. суммарное количество проверок равно 2п. Следовательно, вычис­лительная сложность операции обхода равна О(п). С учетом построения де­рева вычислительная сложность в среднем составит О_ср(п log₂ п).

Предлагаю ознакомиться с аналогичными статьями: