Если граф, для оцениваемого алгоритма содержит циклы, то применяется предварительный метод сжатия циклов и замены их вершинами с эквивалентными им трудоёмкостями.
Напомним, что циклом называется совокупность вершин и дуг, охватываемых дугой обратной связи.
Циклы могут быть многократно вложены друг в друга.
Циклом 1-го ранга называется цикл, не содержащий внутри себя ни одного цикла.
Очевидно, что тело цикла 1-го ранга – ориентированный граф без циклов.
Циклом 2-го ранга называется цикл, содержащий хоть бы один цикл 1-го ранга.
Циклом S-го ранга называется цикл, содержащий внутри себя хотя бы один цикл (S-1)-го ранга и, возможно, циклы меньших рангов.
Процесс сжатия циклов в эквивалентные им по трудоемкости вершины начинается с самых внутренних циклов, т.е. с циклов 1-го ранга.
Поскольку тело такого цикла – ориентированный граф без циклов, то к нему может быть применим сетевой метод оценки трудоемкости, после чего все вершины этого подграфа, за исключением условной вершины цикла легко «сжать» в одну вершину С, присвоив ей трудоемкость . Пусть трудоемкость условной вершины Y равна qy.
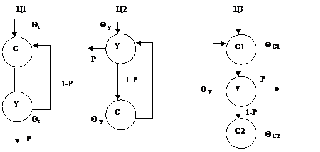
В процессе сжатия циклов 1-го ранга встречаются следующие типы циклов:
Воспользуемся методом марковских цепей для оценки средней трудоемкости qцi каждого типа цикла:
После такого подсчета все вершины цикла Цi сжимаются в одну вершину цикла с трудоемкостью qц и с вероятностями входа и выхода равными 1.
![clip_image001[4] clip_image001[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhx3sT8q4JqM7WJdpa4917JZkbQ-o_kRI_ZbEol2kXPWhbWXndXLRxn29H3L4FADZa4m0l-g2N755iOOSj6wNFaDHOZU-PWISR6aKrt_LwbCNJokYHDMJOYNi5IICU93jJoz0VmcV2kjeQ/?imgmax=800) |
После сжатия циклов 1-го ранга, они исчезают, а циклы 2-го ранга становятся циклами 1-го ранга. Процесс повторяется до тех пор, пока все циклы не будут сжаты и не получен граф без циклов, к которому может быть применен сетевой метод.
Рассмотрим пример:
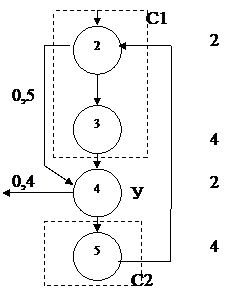
Выделенный в графе цикл является циклом 1-го ранга типа Ц3:
n2=1, n3=0,5n2, так что
qс1=q2n2+q3n3+=2*1+4*0,5=4
n4=ny=0,5n2+n3=0,5*1+0,5=1
По формуле (3): qц3=(4+2+4)/0,4 – 4=21
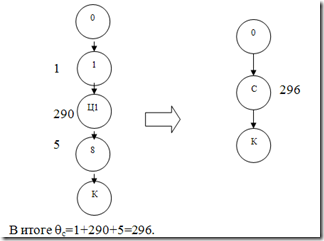
После сжатия исходный граф приобретет вид:
После сжатия граф-схема алгоритма примет вид:


![clip_image003[4] clip_image003[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEif1CBdLNRF5R-RtoXY44acQoFI1a1Z-cDdnK0fbW9hqPBgX35s3K8ZqhGDshL1-ZYRfW7cCEDrWKCrkXEDuR4ajx2k3iHm2Kr1ywfWV88N-kkV9u8WeN4FpQqvqvmxPpwfcnlLHmeLyO4/?imgmax=800)

0 коммент.:
Отправить комментарий