2.5.Оценка максимальной и минимальной трудоемкости алгоритма

Задача оценки минимальной и максимальной ставится следующим образом: для каждой вершины i ГСА известны

q _{i min} и q _{i max} ,а также

P_ij – вероятности перехода от вершины с номером i к вершине с номером j (i=1,2…,К).

Требуется оценить A=q_min и B=q_max – минимальную максимальную трудоемкость алгоритма по ГСА.

На графе без циклов определить маргинальные( то есть минимальную и максимальную) трудоемкости легко.

Обозначим через A_i и B_i – минимальную и максимальную трудоемкости реализации алгоритма на момент прохождения блока i.

A₀=B₀=0,

A_i = min{ A_j }+ q _{i min,}

(j,i) ÎD

B_i= max { B_j }+q _{i max.}

(j,i) ÎD

Дойдя до конечной вершины К, получим:

A=A_k= min{ A_j },

(j,i) ÎD

B=B_k= max{Bj}.

(j,i) ÎD

Рассмотрим пример, иллюстрируемый следующей граф-схемой алгоритма:

A₀=0, B₀=0,

A₁=1, B₁=3,

A₂= A₁+2=3, B₂=B₁+5=8,

A₃=min {A₁,А₂}+1=4, B₃=max{В_1, В₂} +2=10,

A₄=A₂+1=4, B₄=B₂+3=11,

A₅=min{3,4} +1=4, B₅=max{10,11}+4=15,

A₆= min{4,4} +1=5, B₆=max{11,15}+2=17,

A_k=A₆ =5 . B_k=B₆=17.

После этих расчетов исходную схему алгоритма можно заменить графом из одной вершины:

Для графа с циклами также применяется сетевой метод, причем вершинам, соответствующим сжимаемым циклам присваиваются маргинальные оценки :

q_ymin = A_c n_cmin,

q_ymax =B_c n_cmax ,

где A_c и B_c – соответственно минимальные и максимальные трудоемкости тела цикла, а n_cmin и n_cmax –минимальные и максимальные числа прохождения цикла.

Определим эти числа для циклов всех типов:

Цикл типа Ц1:

Здесь n_cmin = 1, A_c= q _cmin + q _ymin.

Чтобы оценить n_cmax, предположим, что число прохождений цикла распределено равномерно на интервале [ n_cmin, n_cmax ] со средним n_c=1/P.

Для определения n_cmax имеем следующее уравнение:

(n_cmin + n_cmax)/2 = n_c, (1+ n_cmax)/2=1/P,

n_cmax=2/P-1.

Далее, B_c= q _cmax + q _ymax , так что

q_min=q _cmin + q _ymin

q_ymax= (q _cmax + q _ymax)*(2/P-1) ( 1 )

Цикл типа Ц2:

Здесь n_cmin=0, qц_2min=q_ymin,

(n_cmin + n_cmax)/2 = n_c, n_cmax/2=1/P-1

1

1-P

n_cmax=2/P-2

так что , qц_2min=q_ymin (2)

q_ц2max= (q _cmax + q _ymax)*(2/P-1)

Цикл типа Ц3:

Здесь, очевидно,

A_c= q _c1min + q _ymin

B_c=(q _c1max + q _ymax)(2/P-1) + q _c2max(1/P-2),

Или по другому:

B_c=2*(q_1max+q_ymax+q_c2max)/P–(q_c1max+q_ymax+2q_c2max) (3)

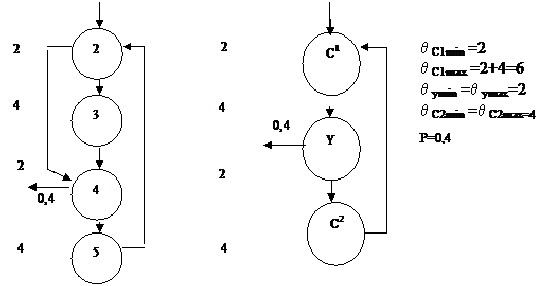
Рассмотрим следующий пример:

q _imin =q _imax=q _i

Цикл типа Ц3:

Используя (3), получим:

A_c=2+2=4,

B_c=2*(6+2+4)/0.4 – (6+2+8) = 44.

После этого цикл заменяем вершиной Ц3:

В результате этих замен получим:

В конечном итоге граф-схема алгоритма имеет вид :

Предлагаю ознакомиться с аналогичными статьями: