Принятие решений в условиях риска

В данном параграфе и далее мы будем предполагать существование функции y=F(x,z), где xX, zZ, yY; X, Z ,Y– соответственно, множества альтернатив (решений), состояний среды и исходов. Особенностью рассматриваемых ниже задач ПР является предположение о неизвестном в момент принятия решения значении параметра Z. Саму функцию F будем называть функцией реализации [10]. Таким образом, функция реализации ставит в соответствие каждой паре вида (x,z), где x - альтернатива, а z - состояние фактора неопределенности, исход y.

Когда говорят о принятии решений в условиях риска, обычно предполагают, что каждой альтернативе соответствует распределение вероятностей на множестве исходов. Если множества альтернатив и исходов конечны, то считаются известными вероятности каждого исхода, возможного при выборе данной альтернативы.

Наглядно связи между альтернативами и исходами можно представить с помощью графа (рисунок 9).

На графе точка 0 означает лицо, принимающее решение (ЛПР). Эта точка соединяется стрелками с теми альтернативами x_i , которые доступны ЛПР в данном акте принятия решения. Далее альтернатива x_i соединяется стрелками с возможными при выборе этой альтернативы исходами. Около каждой такой стрелки может быть указан вес - вероятность наступления соответствующего исхода (очевидно, что сумма весов стрелок, выходящих из одной и той же точки x_i , должна равняться единице). Построенный таким образом граф называется графом связей альтернатив с исходами.

Пример 1.3 (замена вратаря) [10].

На последней минуте хоккейного матча при ничейном счете тренер команды должен принять решение о замене вратаря шестым полевым игроком. Статистика, имеющаяся у тренера, показывает, что в аналогичных условиях в предыдущих встречах замена вратаря в одной шестой части случаев привела к выигрышу, в половине случаев - к ничьей и в одной трети случаев - к поражению. Если же вратарь не заменялся, то в семи случаях из восьми встреча заканчивалась вничью, а в одном случае из восьми команда проигрывала.

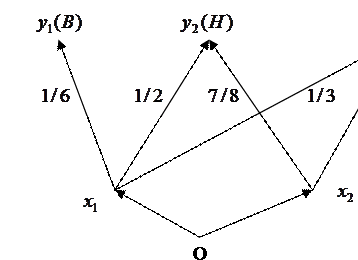
Построим для этой задачи граф связей альтернатив и исходов (Рисунок 10).

Здесь имеются две альтернативы: x₁ - заменить вратаря, x₂ - не делать замены. В любом случае возможны три исхода: выигрыш (B), ничья (H) и поражение (П). Примем за вероятность каждого исхода частоту его появления в предыдущих матчах. Сформулированная задача ПР в условиях риска и приведенный пример 1.3 не позволяют пока понять, где же здесь состояния среды. Какой характер имеет функция реализации F(x,z) и возможно ли вообще ее построение? Оказывается, что язык функции реализации является достаточно общим и позволяет описывать различные ситуации неопределенности, в том числе и рассмотренную выше. Задание функции реализации означает, что при известном z мы по каждому x уже однозначно определяем исход y. Таким образом, зная состояние cреды z , мы должны точно знать, что будет, если мы выберем альтернативу x₁, и каков будет исход при выборе x_2. Введем следующие шесть “состояний cреды”:

z₁: x₁ B, x₂ H р(z₁)=(1/6)(7/8)=7/48;

z₂: x₁ H, x₂ H р(z₂)=(1/2)(7/8)=7/16;

z₃: x₁ П, x₂H р(z₃)=(1/3)(7/8)=7/24;

z₄: x₁ B, x₂П р(z₄)=(1/6)(1/8)=1/48;

z₅: x₁ H, x₂П р(z_z)=(1/2)(1/8)=1/16;

z₆: x₁ П, x₂П р(z₆)=(1/3)(1/8)=1/24.

В правом столбце указаны вероятности соответствующих событий.

Теперь функция реализации может быть задана в виде таблицы 5. Около каждого состояния среды указана вероятность его появления.

Таблица 5

Z X	z1 (7/48)	z2 (7/16)	z3 (7/24)	z4 (1/48)	z5 (1/16)	z6 (`1/24)
x1	В	Н	П	В	Н	П
x2	Н	Н	Н	П	П	П

Решение данной задачи будет приведено ниже.

Рассмотрим теперь задачу ПР в более общем случае , когда имеется n альтернатив x₁,...,x_n и l исходов y₁,...,y_l. В качестве “состояния среды” возьмем множество возможных согласно графу связей альтернатив и исходов отображений z_j: XY, j=1,...,m. В случае конечных множеств X и Y будем иметь m=, где - количество стрелок, исходящих из альтернативы x_i, на графе связей альтернатив и исходов (в нашем примере s₁=3, s₂=2, m=6). Таким образом, каждое “состояние среды” z_j соответствует такому подграфу связей альтернатив и исходов (будем называть его подграфом состояния), в котором из каждой альтернативы x_i исходит только одна стрелка, указывающая, какой исход будет реализован при выборе альтернативы x_i (m - максимально возможное число таких подграфов). Следовательно, как и в примере 3, выбор “состояний cреды” z_j и альтернативы x_i полностью определяет исход - обозначим его через y_j(x_i). Далее, каждому состоянию среды z_j cоответствует вероятность его наступления (вероятность реализации соответствующего подграфа состояния):

p(z_j)=, j=1,...,m,

где p_i(y_j(x_i)) - заданная вероятность наступления исхода y_j при выборе альтернативы x_i. Таким образом, для вычисления p(z_j) достаточно перемножить числа, стоящие около стрелок, входящих в подграф состояния z_j. Теперь таблица, представляющая функцию реализации, уже может быть построена.

Установленная выше возможность представления задачи ПР в условиях риска в форме функции реализации означает, что статистическую неопределенность, проявляющуюся в неоднозначной (вероятностной) связи между средством и результатом, всегда можно интерпретировать, как существование некоторой среды, оказывающей влияние на результат. Методологическое значение этого факта состоит в том, что достаточно широкий класс задач ПР может быть приведен к указанной стандартной форме - форме функции реализации. Отметим также, что многие практические задачи ПР непосредственно формулируются в форме функции реализации. Это, прежде всего, такие задачи, где реально существует среда, влияющая на результат принятия того или иного решения. В качестве примера могут быть указаны задачи принятия оптимальных проектных решений в условиях технологического разброса параметров изделия.

Итак, пусть задана функция реализации y=F(x,z), где множества X, Y, Z, уже не будем предполагать конечными. В условиях полной определенности, как мы видели, задана однозначная связь y=(x), которая, очевидно, и является соответствующей функцией реализации (“состояние среды” Z задано и фиксировано). Основная задача ПР состоит в поиске ядра бинарного отношения R_y в множестве исходов Y.

Будем считать, что задана функция f: Y E, отображающая множество исходов Y на множество вещественных чисел Е. Бинарное отношение R_y задается условием

()R_y f()>f()

(является отношением строгого порядка). Тогда, рассуждая аналогично подразделу1.2.1.1, приходим к выводу, что существует функционал

I : XZE

и задача ПР эквивалентна задаче оптимизации

I(x,z). (3)

В данном случае у функционала I появился новый аргумент z, так как вместо y=(x) имеем в условиях риска в качестве функции реализации зависимость y=F(x,z).

Таким образом, мы использовали здесь критериальный язык для бинарного отношения предпочтения на множестве исходов Y. Более того, исходы y оцениваются в данном случае по однокритериальной схеме, так как задана одна функция f(y) (целевая функция), характеризующая “полезность” исходов.

Таким образом, говоря о задаче ПР, сформулированной в виде (3), мы имеем в виду выбор решения (альтернативы) x в условиях, когда целевая функция задана, но задана не совсем точно - она содержит неопределенный параметр z. Решая задачу (3), мы можем определить x лишь как некоторую функцию параметра z: x=x(z). Если никакой информацией о факторе неопределенности z мы не располагаем, то и результат максимизации функционала I произволен. При наличии статистической неопределенности мы предполагаем, что z - cлучайная величина, закон распределения которой известен.

Методологически важно различать две основные ситуации :

§ исход yY, соответствующий принятому решению x, реализуется многократно;

§ исход yY реализуется однократно.

Так выбор конструктивных параметров изделия, выпускаемого серийно, дает пример многократной реализации исхода одного и того же выбора. Напротив, оптимальный выбор параметров уникального изделия - пример второй ситуации.

Обратимся к методам ПР при наличии многократно реализованного исхода. В этих случаях задачу (3) естественно заменить некоторой вероятностной задачей. Вполне разумным представляется выбор такой альтернативы x, которая максимизирует математическое ожидание критерия, т.е. является решением задачи

I₁(x) (4)

где черта сверху означает математическое ожидание случайной величины I(x,z). Правило выбора оптимальной альтернативы на основе решения задачи оптимизации (4) называется критерием математического ожидания. Если предположить, что функционал I характеризует “полезность” или ”доход”, полученный от решения x и реализовавшегося исхода y, математическое ожидание можно рассматривать как средний доход, и, решая задачу (4), мы фактически максимизируем средний доход.

Пример 1.4.

Вернемся к ситуации, описанной в примере 3 из введения. Обозначим через p вероятность появления контролера (вероятность его непоявления равна, следовательно, 1-p). Функция I(x,z) может быть представлена в виде таблицы 6.

Таблица 6

Z X	z1 (p)	z2 (1-p)
x1	-40	-40
x2	-840	0

В таблице I(x₁,z₁)=-30 и т.д. Имеем теперь:

=p(-40)+(1-p)(-40)=-40;

=p(-840)+(1-p)*0= -840 p.

Следовательно, согласно критерию (4), надо предпочесть первую альтернативу x₁ (брать билет) второй, если -40>-840p, т.е. p>40/8400,048. В противном случае более предпочтительной следует признать альтернативу x₂. Если считать, что каждый троллейбус имеет одинаковые шансы посещения контролером, число троллейбусов равно k,. а число контролеров - r (предполагается, что r<<k), то можно положить, что pr/k. Таким образом, если на 1000 троллейбусов приходится более 48 контролеров, выгоднее брать билет.

Пример 1.5 (продолжение примера о замене вратаря).

Будем численно оценивать исходы игры по получаемым очкам: B - 2 очка, H - 1 очко П - 0 очков. Тогда таблица, задающая функционал I(x,z), получается непосредственно из таблицы 5 и имеет вид таблицы 7.

Таблица 7

Z X	z1 (7/48)	z2 (7/16)	z3 (7/24)	z4 (1/48)	z5 (1/16)	z6 (`1/24)
x1	2	1	0	2	1	0
x2	1	1	1	0	0	0

Аналогично предыдущему примеру вычисляем:

=2(7/48)+1(7/16)+2(1/48)+1(1/16)= 5/6;

=1(7/48)+1(7/16)+1(7/24)=7/8.

Имеем> и поэтому, руководствуясь критерием числа ожидаемых очков, принимаем решение, что в подобных ситуациях нецелесообразно заменять вратаря. “В среднем” такая стратегия приведет к успеху, хотя в каждой конкретной игре, конечно, может реализоваться любой возможный исход.

Упражнения.

а). Решите пример 3 для случая, когда исходы игры по получаемым очкам оцениваются следующим образом: В - 3 очка, Н - 1 очко, П - 0 очков.

б). Указанный в примере 3 критерий (число очков) может быть неадекватен цели принимающего решение. Легко представить себе ситуацию, когда выигрыш оценивают числом t, показывающим, во сколько раз выигрыш важнее ничьей (при этом может быть, что t>2). Определите, при каком t выгоднее предпочесть альтернативу x₁ (заменить вратаря). Ответ: t2,25.

Замена задачи I(x,z)max задачей max - не единственный способ перехода к статистической постановке. Можно поступить и иначе. Например, определенную роль может играть дисперсия критериальной функции I. И, может быть, имеет смысл иногда поступиться немного значением математического ожидания для уменьшения возможного разброса результатов, т.е. уменьшения значения дисперсии:

I₂(x)-k. (5)

Здесь - дисперсия случайной величины I(x,z); k - заданная постоянная. Эту постоянную целесообразно интерпретировать как степень несклонности к риску. Действительно, k определяет “степень важности” дисперсии по отношению к математическому ожиданию случайной величины I. Увеличение значения k приводит, вообще говоря, к уменьшению “среднего дохода” , но зато уменьшается и вероятность отклонения от среднего дохода (в том числе, в сторону его уменьшения). Таким образом, чем больше k, тем менее склонно к риску лицо, принимающее решение. Критерий (5) обычно называется критерием ожидаемое значение - дисперсия.

Трудности решения задач (4), (5) связаны с высокой трудоемкостью вычисления математического ожидания. Мы должны сначала задать значения компонент вектора x и лишь затем провести усреднение - операцию, связанную, вообще говоря, с вычислением многомерных интегралов и потому требующую значительных затрат машинного времени. Иначе говоря, в отличие от детерминированной постановки задачи оптимизации, функционалы I₁, I₂ не заданы в явном виде как функции x. Все это часто заставляет заменять эти задачи на другие. Если решение задачи

I(x,z)

при фиксированном значении случайного параметра z сравнительно просто определяется, то вместо критерия математического ожидания применяется следующий критерий

I₃(x) I(x,,

где - математическое ожидание случайной величины z. Оценка исходов y по векторному отображению

I: XE^m, I=(I₁(x),...,I_m(x)),

где функционалы I_i также зависят от определенных факторов, приводит к аналогичным конструкциям.

Таким образом, в случае многократной реализации исхода принятого решения проблема выбора мало чем отличается от ситуаций, в которых случайные факторы отсутствуют. Дополнительные сложности здесь носят чисто вычислительный характер и связаны с необходимостью выполнения операции усреднения.

Ситуация становится существенно более сложной, если исход принятого решения реализуется однократно (“одноразовое использование решения”). Такой случай характерен, в частности, при решении задач оптимального выбора параметров уникальных изделий, например, мостов, ирригационных сооружений и т.д. При этом информация о статистических характеристиках факторов неопределенности, даже если она и имеется, не имеет никакого смысла : какова бы ни была вероятность того, что значение некоторого числового параметра неопределенности будет равно 10¹⁰ или 10^-10, мы ничего не сможем сказать о значении функционала I(x,z), которое реализуется в действительности при конкретном выборе x. Здесь мы в силу уникальности ситуации уже не можем “ рассчитывать на средний случай”. Такого типа задачи ПР необходимо решать особыми нестатистическими методами.

Предлагаю ознакомиться с аналогичными статьями:

ТПР

• Принятие решения в условиях неопределенности
• Принятие решений при наличии неопределенных факторов
• Многокритериальные задачи ПР в условиях определенности
• Однокритериальные задачи ПР в условиях определенности.
• Классификация проблем принятия решений